Определение
функции распределения дискретной случайной
величины и построение ее графика ~ Распределение
дискретного случайного вектора ~ Библиотека
стандартных распределений
Определение функции распределения
дискретной случайной величины и построение ее
графика
Дискретная случайная величина  с вероятностями с вероятностями  может быть задана распределением
- таблицей вида может быть задана распределением
- таблицей вида
Такие таблицы в среде Mathcad удобно хранить в виде
матрицы размерности 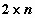 . .
Функция распределения случайной величины,
имеющей приведенное выше распределение, имеет
вид
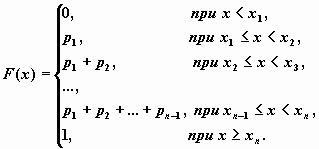
В приведенном ниже примере показано, как в Mathcad
можно определить дискретную случайную величину,
ее функцию распределения и построить график
функции распределения.
ПРИМЕР 1. Определим случайную
величину, заданную приведенным ниже
распределением. Определим в Mathcad эту случайную
величину, определим ее функцию распределения и
построим график функции распределения.
Дискретная случайная величина имеет
распределение
Распределение дискретного
случайного вектора
Распределение дискретного случайного вектора 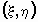
| |
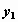 |
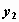 |
... |
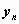 |
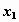 |
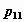 |
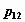 |
... |
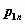 |
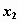 |
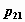 |
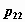 |
... |
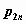 |
| ... |
... |
... |
... |
... |
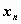 |
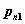 |
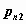 |
... |
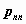 |
также удобно хранить в матрице размерности 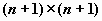 . Первому элементу
первой строки этой матрицы присваивается
нулевое значение, остальные элементы первой
строки содержат значения случайной компоненты . Первому элементу
первой строки этой матрицы присваивается
нулевое значение, остальные элементы первой
строки содержат значения случайной компоненты 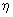 , элементы первого
столбца - значения случайной компоненты , элементы первого
столбца - значения случайной компоненты 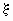 , а остальные элементы -
соответствующие вероятности: элемент,
расположенный в , а остальные элементы -
соответствующие вероятности: элемент,
расположенный в 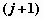 -м столбце -м столбце 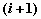 -й строки содержит значение
вероятности -й строки содержит значение
вероятности 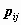 того, что
случайный вектор того, что
случайный вектор 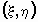 принимает значение
принимает значение 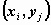 . .
В приведенном ниже примере показано, как в Mathcad
можно определить двумерный случайный вектор.
ПРИМЕР 2. Определим в Mathcad двумерный
случайный вектор. Случайный вектор задан
следующей таблицей:
| |
1 |
3 |
5 |
7 |
| 2 |
0.01 |
0.01 |
0.17 |
0.01 |
| 4 |
0.1 |
0.2 |
0.1 |
0.2 |
| 6 |
0.02 |
0.05 |
0.09 |
0.04 |
Библиотека стандартных распределений
Для вычислений со случайными величинами
(непрерывными и дискретными) в Mathcad есть богатая
библиотека встроенных функций наиболее
распространенных стандартных распределений.
Каждое распределение представлено в библиотеке
тремя функциями - плотностью вероятностей для
непрерывных распределений и функцией,
вычисляющей вероятность заданного значения - для
дискретных распределений, функцией
распределения и функцией, обратной к функции
распределения.
Например, для нормального распределения - это
функции 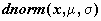 , , 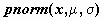 и и 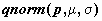 . Значением функции . Значением функции 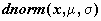 является значение в
точке является значение в
точке 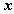 плотности
вероятностей случайной величины плотности
вероятностей случайной величины 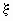 , имеющей нормальное
распределение с математическим ожиданием , имеющей нормальное
распределение с математическим ожиданием 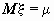 и дисперсией и дисперсией 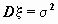 ; значение функции ; значение функции 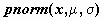 - значение
функции распределения этой же случайной
величины - значение
функции распределения этой же случайной
величины 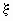 ; значением
функции ; значением
функции 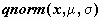 является
решение уравнения является
решение уравнения 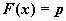 ,
где ,
где 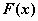 - функция
распределения, определенная функцией - функция
распределения, определенная функцией 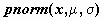 , т.е.
значением , т.е.
значением 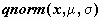 является
квантиль уровня является
квантиль уровня 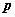 нормально распределенной случайной
величины. Имена всех встроенных функций,
определяющих плотности вероятностей, начинаются
с буквы нормально распределенной случайной
величины. Имена всех встроенных функций,
определяющих плотности вероятностей, начинаются
с буквы 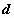 , определяющих
функции распределения - с буквы , определяющих
функции распределения - с буквы 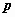 , определяющих квантили - с
буквы , определяющих квантили - с
буквы 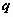 . .
Ниже приведен список всех распределений,
представленных в библиотеке Mathcad, и имена
соответствующих функций:
бета-распределение - 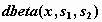 , , 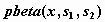 , , 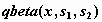 ; ;
биномиальное распределение - 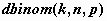 , , 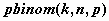 , , 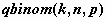 ; ;
распределение Коши- 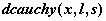 , , 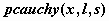 , ,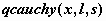 ; ;
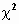 -распределение- -распределение-
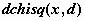 , , 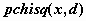 , , 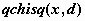 ; ;
экспоненциальное распределение - 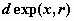 , , 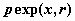 , , 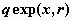 ; ;
распределение Фишера, F-распределение - 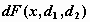 , , 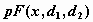 , , 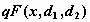 ; ;
Гамма-распределение - 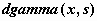 , , 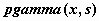 , , 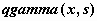 ; ;
геометрическое распределение - 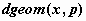 , , 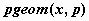 , , 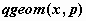 ; ;
логнормальное распределение - 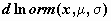 , , 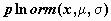 , , 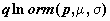 ; ;
логистическое распределение - 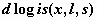 , , 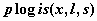 , , 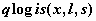 ; ;
отрицательное биномиальное распределение
- 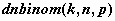 , , 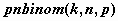 , , 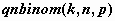 ; ;
нормальное распределение - 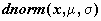 , , 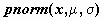 , , 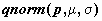 ; ;
распределение Пуассона - 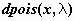 , , 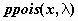 , , 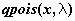 ; ;
распределение Стьюдента - 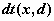 , , 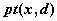 , , 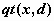 ; ;
равномерное распределение - 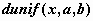 , , 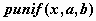 , , 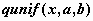 ; ;
распределение Вейбулла - 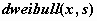 , , 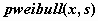 , , 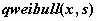 . .
В приведенном ниже примере построены графики и
выполнены вычисления, демонстрирующие некоторые
основные свойства функций, связанных со
стандартным нормальным распределением 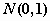 . .
ПРИМЕР 3. Построим график плотности
вероятностей и функции распределения для
стандартного нормального распределения.
Вычислим квантиль a уровня 0.1 и значение
функции распределения в точке x = a (т.е.
проверим правильность вычисления квантили).
Кроме перечисленных функций, в библиотеке
встроенных функций Mathcad есть функция Лапласа
(интеграл ошибок) 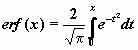 . .
Для вычисления числовых характеристик
дискретных и непрерывных случайных величин в
Mathcad есть операторы интегрирования и
дифференцирования вычисления конечных сумм и
суммирования рядов, которые могут быть выполнены
щелчком мыши по кнопке в панели  и заполнением
соответствующих помеченных полей. и заполнением
соответствующих помеченных полей.
|

