  Mathcad
применяет для решения систем уравнений и
неравенств итерационный метод
Левенберга-Маркардта. Этот метод Mathcad
заимствован из свободно распространяемого
пакета алгоритмов MINPACK, разработанного и
издаваемого Аргоннской Национальной
Лабораторией в Аргонне, Штат Иллинойс. Этот пакет
подробно описан в Users Guide to Minpack I, by Jorge J. More, Burton
S. Garbow, and Kenneth E. Hillstrom, Argonne National Laboratory publication ANL-80-74,
1980.
Вектор невязки
Алгоритм MINPACK пытается найти нули или, в
наихудшем случае, минимизировать сумму
квадратов компонент вектора значений нескольких
функций, зависящих от нескольких переменных при
заданных неравенствами ограничениях. Вектор
функций, используемый Mathcad, есть вектор
невязки, компоненты которого представляют
собой невязки в отдельных уравнениях или
неравенствах. Определение невязок таково:
constraints;components of error vector for
error = left_side - right_side
- Для неравенств <, >,
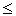 , или , или 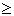 : :
error = 0
если неравенство истинно, иначе
error = left_side - right_side
В Mathcad реализован алгоритм
Левенберга-Маркардта. Когда решение ищется в
поле комплексных чисел, Mathcad рассматривает
вещественные и мнимые части как отдельные
переменные в алгоритме и создает из комплексного
уравнения два вещественных, отделяя
вещественную и мнимую части исходного уравнения.
Алгоритм метода Левенберга-Маркардта
Метод Левенберга-Маркардта является
квазиньютоновским методом (разновидностью
градиентного метода). На каждом шаге алгоритма
Mathcad вычисляет первые частные производные
невязок относительно переменных, по которым
ищется решение, и составляет соответствующую
матрицу Якоби. Обычно Mathcad может определить
следующее приближение, вычисляя шаг
Гаусса-Ньютона s по каждой переменной. В
матричной нотации Mathcad решает матричное
уравнение:
J s = -f(x) s = -f(x)
В этом уравнении J есть матрица Якоби, s
— вектор приращения неизвестных, x — текущий
вектор приближений к неизвестным. На первом шаге x
— вектор начальных приближений; на каждом
последующем шаге новый x равен сумме старого x
и приращения s. Отметим, что на каждом шаге
необходимо обращать матрицу Якоби J.
Вычисление очередного приближения не всегда
возможно, например, когда матрица Якоби
необратима, или когда число ограничений больше
числа неизвестных. В подобных случаях Mathcad
использует дополнительное условие минимизации
следующей величины:
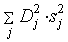
Здесь D есть вектор весов, составленный из
норм столбцов матрицы Якоби. В этих случаях
вектор приращений s вычисляется как из
условия минимизации, так и из условия
удовлетворения уравнению Ньютона с матрицей
Якоби.
Метод Левенберга-Маркардта неприменим в
случае, когда неизвестных меньше, чем
ограничений. В этих случаях Mathcad возвращает
ошибку “слишком мало ограничений” .
Критерии окончания итераций
Метод Левенберга-Маркардта заканчивается,
когда выполняется один из следующих критериев
окончания:
- Когда больше невозможно заметно уменьшить
норму вектора невязки. В этом контексте
“заметно” означает больше, чем больший из TOL и TOL
 |error_vector|.
Этот критерий останавливает процесс решения,
когда невязки не могут быть уменьшены далее. |error_vector|.
Этот критерий останавливает процесс решения,
когда невязки не могут быть уменьшены далее.
- Когда норма s становится относительно малой.
В этом методе “относительно малый” означает
норму меньшую, чем больший из TOL и TOL
 |v|. Этот критерий
останавливает процесс решения, когда не
находится нового определенного приближения. |v|. Этот критерий
останавливает процесс решения, когда не
находится нового определенного приближения.
Когда Mathcad достигает одного из этих условий
окончания, то он проверяет величину вектора
невязки и возвращает ответ:
- Если величина вектора невязки меньше или равна
TOL, то Mathcad возвращает в качестве ответа значения
неизвестных.
- Если система решается функцией Find, и
величина вектора невязки оказывается больше, чем
TOL, то Mathcad отмечает систему уравнений сообщением
об ошибке “решение не найдено”. Если система
решается функцией Minerr, то Mathcad возвращают
решение в любом случае, даже если вектор невязки
не близок к нулю.
Если процесс поиска решения заканчивается
вследствие исчерпания заданного числа итераций,
а ответ еще не найден, то состояния Find или Minerr
отмечаются сообщением об ошибке “отсутствует
сходимость”.
Во всех случаях, когда процесс решения
заканчивается, Mathcad присваивает переменной ERR
величину вектора невязки.
Метод Левенберга-Маркардта, используемый Mathcad
Для того, чтобы сделать метод
Левенберга-Маркардта более эффективным, Mathcad
применяет следующие модификации исходного
метода:
- При первой остановке процесса итераций в точке,
не являющейся решением, Mathcad добавляет малое
случайное смещение к неизвестным и вновь
начинает итерации. Этот прием позволяет
избегнуть зависания
процесса итераций в локальных минимумах и
подобных особенностях рельефа модуля функции —
левой части системы уравнений. Mathcad делает это
только один раз в первой встреченной подобной
точке.
- Если в решаемой системе присутствуют
неравенства, Mathcad вначале решает только
подсистему, состоящую из неравенств, а потом
добавляет уравнения и пытается решить полную
систему. Это эквивалентно выбору начального
приближения в области, где все неравенства
удовлетворены.
  
|

