  Функция
Mathcad root использует метод секущей для
отыскания корней уравнений.
Этот раздел описывает, как Mathcad вычисляет root( f(x),x).
В этом описании estimate0, estimate1
и так далее, обозначают последовательные
приближения Mathcad к ответу. Только последняя
оценка, если она удовлетворяет требованиям Mathcad,
становится доступной пользователю.
Чтобы вычислить корень f(x) с
использованием начального приближения x, Mathcad
следует следующему алгоритму:
- Если |f(x)|< TOL, то x — корень и это есть
значение функции root.
- Положить n = 1. Если x
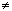 0, то положить h = TOL 0, то положить h = TOL x, иначе положить h =
TOL. Взять в качестве начальных значений: x, иначе положить h =
TOL. Взять в качестве начальных значений:
estimate0 = x
estimate1 = x+h
- Увеличить n на единицу. Вычислить прямую
линию, соединяющую точки (estimaten-2 ,f(estimaten-2))
и (estimaten-1 ,f(estimaten-1)).
Присвоить значение абсциссы точки пересечения
этой прямой с осью абсцисс.
- Если f(estimaten) < TOL, то estimaten
есть значение функции корня. Иначе перейти к шагу
3.
Число итераций, которое Mathcad выполняет для
поиска одного значения функции root, ограничено.
Если за заданное число итераций ответ не найден,
то функция root отмечается сообщением об
ошибке “отсутствует сходимость”.
  
|

