Список встроенных функций

Mathcad оценивает численно определенные интегралы, используя алгоритм Ромберга. Метод Ромберга ускоряет сходимость последовательности метода трапеций или метода прямоугольников к интегралу, экстраполируя последовательность оценок величины интеграла и ширины шага интегрирования.

Этот раздел описывает то, как Mathcad вычисляет интеграл от f(x) по интервалу от a до b. В этом описании , , и так далее, представляют собой внутренние приближения Mathcad к ответу. Только последнее такое приближение, удовлетворяющее условиям допустимости Mathcad, становится доступным пользователю.

Шаги вычисления интеграла от f(x) от a до b:

• Вычисляется первая оценка интеграла методом трапеций с шагом интегрирования, равным всему интервалу интегрирования:

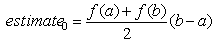
Вторая оценка методом трапеций проводится с двумя шагами интегрирования половинной ширины . Для того, чтобы инициировать алгоритм, вычисляются первые три оценки, подразделяющие интервал интегрирования на один, два и четыре шага интегрирования соответственно.

• Строится полином по величине шага интегрирования, приближающий последовательность оценок интеграла методом трапеций, вычисленных к текущему моменту. Значение этого полинома для нулевой величины шага интегрирования представляет собой оценку Ромберга для искомого интеграла.
• Две последних оценки Ромберга сравниваются согласно следующему правилу (здесь reltol есть наибольшее из TOL и TOL|estimate_n|:

|estimate_n - estimate_n-1| < reltol

• Если две последних оценки удовлетворяют этому тесту, то проверяется также, удовлетворяют ли ему также и . Если это так, то последняя оценка Ромберга используется как значение интеграла. Если нет, то число интервалов удваивается и происходит переход к предыдущему этапу.

Mathcad ограничивает число итераций согласно вышеописанной процедуре. Если описанная процедура не сходится за заданное число итераций, или если подинтегральное выражение имеет особенность в одной или обеих граничных точках интервала интегрирования, то Mathcad переходит к методу Ромберга с открытыми концами.

В методе Ромберга с открытыми концами предварительные оценки получаются с использованием значений функции в средних точках интервалов интегрирования без необходимости оценки функции в конечных точках a и b. (полное описание см. Handheld Calculator Evaluates Integrals, WilliamKahan,Ph.D., в Hewlett-Packard Journal, August 1980). Точки вычисления функции сосредоточены около концов интервала интегрирования, там, где подинтегральные выражения являются сингулярными или имеют бесконечную производную, и, следовательно, изменяются наиболее быстро. Число интервалов интегрирования утраивается при каждом шаге.

Метод Ромберга с открытыми концами реализуется следующим алгоритмом:

• Вычисляется оценка интеграла методом прямоугольников, используя значение функции в средней точке интервала интегрирования:

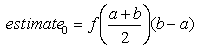
Для вычисления второй оценки используются три значения функции, для третьей — девять значений, и т. д.

• Для каждого шага, следующего за третьим, применяется ускорение сходимости по Ромбергу.
• Сравниваются две последних оценки Ромберга согласно следующему правилу ( reltol есть наибольшее из TOL и TOL|estimate_n|:

|estimate_n - estimate_n-1| < reltol

• Если две последних оценки удовлетворяют этому тесту, то самая последняя оценка есть значение интеграла, вычисленное по методу Ромберга с открытыми концами. Иначе число интервалов утраивается и происходит возврат к предыдущему этапу.

Снова Mathcad ограничивает число шагов алгоритма. Если за заданное число шагов ответ не получен, то интеграл отмечается сообщением об ошибке “отсутствует сходимость”.

Mathcad может вычислять разнообразные интегралы, имеющие особенности подинтегрального выражения в одном или в обоих концах интервала  интегрирования.

Вычисление таких интегралов оказывается часто более медленным, чем интегралов с регулярными подинтегральными выражениями. Для малых значений TOL последовательность оценок интеграла может не сойтись, даже если интеграл имеет конечное значение.

В общем случае Mathcad не может интегрировать функции, имеющие особенности во внутренних точках интервала интегрирования. Присутствие значительного числа точек разрыва функции и ее производной (например, ступеньки или пилообразная функция) на интервале интегрирования также могут вести к расходимости последовательности оценок интеграла. Если расположение особенностей и разрывов в подинтегральном выражении известно заранее, то часто можно получить правильную числовую оценку, разделив интервал интегрирования на подинтервалы с особенностями в граничных точках и вычисляя искомый интеграл как сумму интегралов по этим подинтервалам. График подинтегрального выражения может помочь найти его особенности.

Список встроенных функций