  Оператор
вычисления производной Mathcad использует для
вычисления производных порядка от 0 до 5
включительно модифицированный метод Риддера.
Оператор производной Mathcad не вычисляет
производные порядка выше 5, так что для
вычисления производных высших порядков
необходимо использовать соответствующие
суперпозиции оператора дифференцирования.
Вычисления согласно модифицированному методу
Риддера начинаются с определения начального
значения шага дифференцирования h и
построения треугольного массива оценок. Это
происходит следующим образом:
- Mathcad вычисляет первую оценку производной в этом
массиве, используя аппроксимацию разделенной
разностью n+1- го порядка.
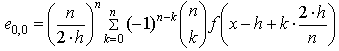
- Остальные оценки из первой строки таблицы
вычисляются с использованием разделенных
разностей с уменьшенным размером шага:
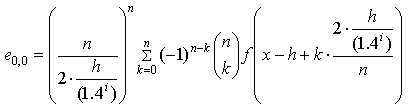
- Остальные элементы в таблице оценок вычислены с
использованием взвешенных средних значений
предыдущих элементов:
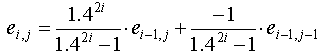
- Ошибка такой оценки значения производной есть:
erri,j = max( |ei,j - ei-1,j|,
|ei,j - ei-1,j-1|)
- Пусть errmin есть наименьшая из , и пусть der
есть оценка значения производной,
соответствующая errmin. Тогда, если:
errmin < max( E, E der) der)
где E - малая величина, зависящая от порядка,
то Mathcad возвращает der как значение
производной. Если нет, то Mathcad отмечает
производную сообщением “отсутствует
сходимость” .
Заметим, что любой алгоритм численного
дифференцирования является неустойчивым по
отношению к ошибкам, вносимым в вычисления
округлением либо усечением. Особенно сильно это
обстоятельство проявляется вблизи точек разрыва
и других особенностей функции. Обычно алгоритм
Риддера дает 7 или 8 верных значащих цифр значения
первой производной при условии, что точка, в
которой вычисляется производная, не слишком
близка к какой-либо особенности функции.
Точность этого алгоритма убывает примерно на
одну значащую цифру на единицу увеличения
порядка производной.
  
|

