Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример
4
Пример 1. Глобальная интерполяция функции Рунге.

Пример 2. Кусочно-линейная интерполяция функции Рунге.

Пример 3. Построение
параболического сплайна.
Пусть дан фрагмент таблицы значений функции:
Требуется построить параболический сплайн
дефекта 1.
Так как строится сплайн 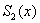 , то он
будет представлен двумя полиномами 2-ой степени: , то он
будет представлен двумя полиномами 2-ой степени:
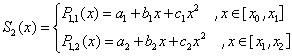
Функция 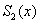 должна удовлетворять
условиям: должна удовлетворять
условиям:
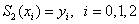 - это есть условие
интерполяции; - это есть условие
интерполяции;
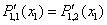 - это есть условие
непрерывности первой производной. - это есть условие
непрерывности первой производной.
Таким образом, получили 5 условий для
нахождения 6-сти неизвестных. Два условия
дополнительно накладывают на сплайн в граничных
точках.
Возьмем, например дополнительное граничное
условие следующего вида 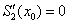 . .
Тогда получим систему уравнений относительно
неизвестных коэффициентов 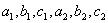 : :
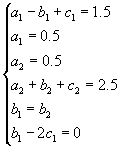
Эта система легко решается: 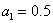 , , 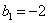 , , 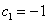 , , 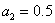 , , 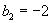 , , 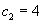 . .
Таким образом, 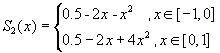 . .
Теоретическая справка

Пример 4.
Построение сплайн-интерполяции.

|

