Глобальная интерполяция ~ Кусочно-полиномиальная интерполяция ~ Определение интерполяционного сплайна ~ Дефект сплайна ~ Оценка
погрешности интерполяции функции кубическими
сплайнами
Глобальная и кусочно-полиномиальная
интерполяция. Пусть функция f(x)
интерполируется на отрезке [a,b]. Метод решения
этой задачи с помощью единого многочлена 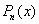 для всего отрезка называют глобальной
полиномиальной интерполяцией. В
вычислительной практике такой поход применяется
редко в силу различных причин. Одна из причин v
необходимо задать стратегию выбора узлов при
интерполяции функции f многочленами все
возрастающей степени n.
для всего отрезка называют глобальной
полиномиальной интерполяцией. В
вычислительной практике такой поход применяется
редко в силу различных причин. Одна из причин v
необходимо задать стратегию выбора узлов при
интерполяции функции f многочленами все
возрастающей степени n.
Теорема Фабера. Какова бы ни была стратегия
выбора узлов интерполяции, найдется непрерывная
на отрезке [a,b] функция f, для которой 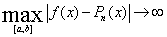 при при 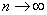 . Таким
образом, теорема Фабера отрицает существование
единой для всех непрерывных функций стратегии
выбора узлов. Проиллюстрируем сказанное
примером. . Таким
образом, теорема Фабера отрицает существование
единой для всех непрерывных функций стратегии
выбора узлов. Проиллюстрируем сказанное
примером.
Предположим, что выбираем равноотстоящие узлы,
то есть 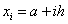 , i = 0,1,...n, где , i = 0,1,...n, где 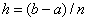 . Покажем, что для
функции Рунге такая стратегия является
неудачной. . Покажем, что для
функции Рунге такая стратегия является
неудачной.

ПРИМЕР 1. Глобальная
интерполяция функции Рунге.
На практике чаще используют кусочно-полиномиальную
интерполяцию: исходный отрезок разбивается
на части и на каждом отрезке малой длины исходная
функция заменяется многочленом невысокой
степени. Система Mathcad предоставляет возможность
аппроксимации двумя важными классами функций:
кусочно-линейной и сплайнами.
При кусочно-линейной интерполяции узловые
точки соединяются отрезками прямых, то есть
через каждые две точки 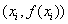 , , 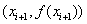 проводится полином первой степени.
проводится полином первой степени.

ПРИМЕР 2. Кусочно-линейная
интерполяция функции Рунге.
Как видно из приведенного примера этот способ
приближения также имеет недостаток: в точках
"стыка" двух соседних многочленов
производная, как правило, имеет разрыв.
Если исходная функция была гладкой и требуется,
чтобы и аппроксимирующая функция была гладкой,
то кусочно-полиномиальная интерполяция
неприемлема. В этом случае применяют сплайны v
специальным образом построенные гладкие
кусочно-многочленные функции.
Интерполяция сплайнами. Пусть
отрезок [a,b] разбит точками на n частичных
отрезков 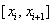 . Сплайном степени m
называется функция . Сплайном степени m
называется функция 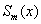 , обладающая следующими
свойствами: , обладающая следующими
свойствами:
1) функция 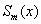 непрерывна на отрезке [a,b]
вместе со своими производными до некоторого
порядка p. непрерывна на отрезке [a,b]
вместе со своими производными до некоторого
порядка p.
2) на каждом частичном отрезке 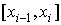 функция
совпадает с некоторым алгебраическим
многочленом функция
совпадает с некоторым алгебраическим
многочленом 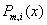 степени m. степени m.
Разность m-p между степенью сплайна и
наивысшим порядком непрерывной на отрезке [a,b]
производной называют дефектом сплайна.
Кусочно-линейная функция является сплайном
первой степени с дефектом, равным единице.
Действительно, на отрезке [a,b] сама функция 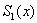 (нулевая производная) непрерывна. В то же время на
каждом частичном отрезке
(нулевая производная) непрерывна. В то же время на
каждом частичном отрезке 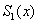 совпадает с
некоторым многочленом первой степени. совпадает с
некоторым многочленом первой степени.

ПРИМЕР 3. Построение
параболического сплайна.
Наиболее широкое распространение получили
сплайны 3 степени (кубические сплайны) 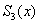 с
дефектом равным 1 или 2. Система для осуществления
сплайн-интерполяции кубическими полиномами
предусматривает несколько встроенных функций.
Одна из них рассмотрена в примере. с
дефектом равным 1 или 2. Система для осуществления
сплайн-интерполяции кубическими полиномами
предусматривает несколько встроенных функций.
Одна из них рассмотрена в примере.

ПРИМЕР 4 . Построение
сплайн-интерполяции.
Погрешность приближения кубическими
сплайнами. Пусть функция f имеет на
отрезке [a,b] непрерывную производную
четвертого порядка и 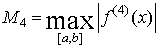 . Тогда для
интерполяционного кубического сплайна
справедлива оценка погрешности: . Тогда для
интерполяционного кубического сплайна
справедлива оценка погрешности: 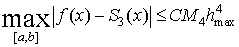 . .

|

