Пример 1 ~ Пример 2 ~ Пример 3
Пример 1. Решение задачи методом Эйлера.
Применяя метод Эйлера, найти решение задачи
Коши: 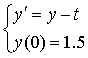 в трех
последовательных точках в трех
последовательных точках 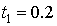 , , 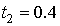 , , 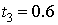 . Найти точное решение задачи и
найти величину абсолютной погрешности в
указанных точках. . Найти точное решение задачи и
найти величину абсолютной погрешности в
указанных точках.
Возьмем шаг 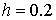 Используя
расчетную формулу Эйлера, найдем приближенное
решение задачи Коши: Используя
расчетную формулу Эйлера, найдем приближенное
решение задачи Коши:
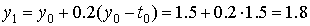 , , 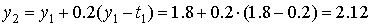 , , 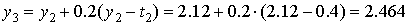 . .
Таким образом, получили численное решение
задачи Коши с шагом 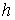 : :
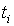 |
0 |
0.2 |
0.4 |
0.6 |
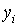 |
1.5 |
1.8 |
2.12 |
2.464 |
В этой задаче легко находится точное решение,
например, методом вариации постоянной:
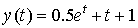 . Вычислим
значения точного решения в указанных точках. . Вычислим
значения точного решения в указанных точках.
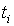 |
0 |
0.2 |
0.4 |
0.6 |
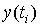 |
1.5 |
1.811 |
2.146 |
2.511 |
Абсолютную погрешность вычислим так: 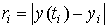 . Тогда . Тогда 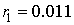 , , 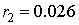 , , 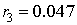 . Таким образом, максимальная
величина погрешности равна . Таким образом, максимальная
величина погрешности равна 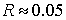 . .
Теоретическая справка

Пример 2. Оценка погрешности по правилу Рунге.

Пример 3. Решение задачи усовершенствованным методом
Эйлера.
Выполнить 1 шаг длины 0.4 с использованием
усовершенствованного метода Эйлера для решения
задачи Коши:
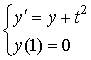 . .
Зададим шаг 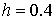 . Тогда решение
в точке 1.4 находится так: . Тогда решение
в точке 1.4 находится так:
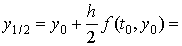 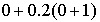 = = 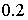
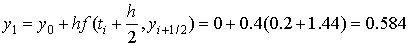
Таким образом 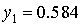 . .
Теоретическая справка

|

