Постановка задачи Коши ~ Численное решение задачи Коши методом
Эйлера ~ Оценка погрешности метода
Эйлера ~ Правило Рунге ~ Модификации
метода Эйлера второго порядка точности ~ Решение систем дифференциальных уравнений
методом Эйлера
Постановка задачи Коши для
дифференциального уравнения первого порядка.
Пусть дано дифференциальное уравнение первого
порядка 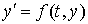 . Требуется найти функцию . Требуется найти функцию 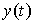 ,
удовлетворяющую при ,
удовлетворяющую при 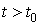 дифференциальному уравнению и при дифференциальному уравнению и при
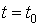 начальному условию
начальному условию 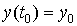 . .
Теорема существования и единственности
задачи Коши. Пусть функция 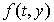 определена и
непрерывна на множестве точек определена и
непрерывна на множестве точек 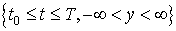 . Предположим
также, что она удовлетворяет условию Липшица: . Предположим
также, что она удовлетворяет условию Липшица: 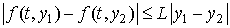 для всех для всех
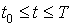 и
произвольных и
произвольных 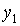 , , 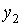 , где , где 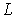 - некоторая константа (постоянная
Липшица). Тогда для каждого начального значения - некоторая константа (постоянная
Липшица). Тогда для каждого начального значения 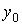 существует единственное решение
существует единственное решение 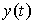 задачи Коши,
определенное на отрезке задачи Коши,
определенное на отрезке 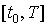 . .
Геометрически задача интегрирования
дифференциальных уравнений состоит в нахождении
интегральных кривых, которые в каждой своей
точке имеют заданное направление касательной.
Заданием начального условия мы выделяем из
семейства решений ту единственную кривую,
которая проходит через фиксированную точку 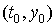
Численное решение задачи Коши методом
Эйлера.
Численное решение задачи Коши состоит в
построении таблицы приближенных значений 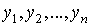 в точках в точках
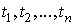 .
Точки .
Точки 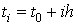 , ,
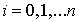 называются узлами сетки, а величина
называются узлами сетки, а величина 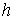 - шагом сетки. В
основе построения дискретной задачи Коши лежит
тот или иной способ замены дифференциального
уравнения его дискретным аналогом. Простейший
метод основан на замене левой части уравнения
правой разностной производной: - шагом сетки. В
основе построения дискретной задачи Коши лежит
тот или иной способ замены дифференциального
уравнения его дискретным аналогом. Простейший
метод основан на замене левой части уравнения
правой разностной производной: 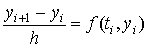 . Разрешая
уравнение относительно . Разрешая
уравнение относительно 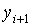 , получаем расчетную
формулу метода Эйлера: , получаем расчетную
формулу метода Эйлера: 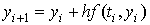 , , 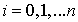 . .

ПРИМЕР 1. Решение задачи методом
Эйлера.
Численный метод называется явным, если
вычисление решения в следующей точке 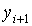 осуществляется по явной формуле. Метод
называется одношаговым, если вычисление
решения в следующей точке
осуществляется по явной формуле. Метод
называется одношаговым, если вычисление
решения в следующей точке 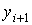 производится с использованием только одного
предыдущего значения
производится с использованием только одного
предыдущего значения 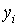 . Метод
Эйлера является явным одношаговым методом. . Метод
Эйлера является явным одношаговым методом.
Оценка погрешности метода Эйлера.
Локальной погрешностью метода называется
величина 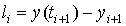 . Найдем величину локальной
погрешности метода Эйлера: . Найдем величину локальной
погрешности метода Эйлера: 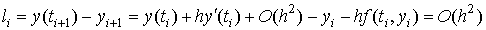 , при
условии, что , при
условии, что 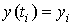 . Другими словами . Другими словами 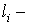 погрешность, которую допускает за один шаг метод,
стартующий с точного решения. Глобальной
погрешностью (или просто погрешностью)
численного метода называют сеточную функцию
погрешность, которую допускает за один шаг метод,
стартующий с точного решения. Глобальной
погрешностью (или просто погрешностью)
численного метода называют сеточную функцию 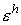 со
значениями со
значениями 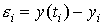 в узлах. В качестве меры
абсолютной погрешности метода примем величину в узлах. В качестве меры
абсолютной погрешности метода примем величину 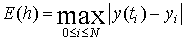 .
Можно показать, что для явных одношаговых
методов из того, что локальная погрешность имеет
вид .
Можно показать, что для явных одношаговых
методов из того, что локальная погрешность имеет
вид 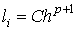 следует, что следует, что 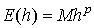 , где , где 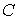 и M
- некоторые константы. Таким образом, метод
Эйлера является методом первого порядка
точности. Для нахождения решения задачи Коши с
заданной точностью и M
- некоторые константы. Таким образом, метод
Эйлера является методом первого порядка
точности. Для нахождения решения задачи Коши с
заданной точностью 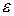 требуется найти такое
приближенное решение требуется найти такое
приближенное решение 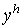 , для
которого величина глобальной погрешности , для
которого величина глобальной погрешности 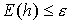 .
Так как точное решение задачи неизвестно,
погрешность оценивают с помощью правила
Рунге. .
Так как точное решение задачи неизвестно,
погрешность оценивают с помощью правила
Рунге.
Правило Рунге оценки погрешностей. Для
практической оценки погрешности проводят
вычисления с шагами h и h/2. За оценку погрешности
решения, полученного с шагом h/2, принимают
величину, равную 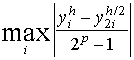 , где p - порядок метода. , где p - порядок метода.

ПРИМЕР 2. Оценка погрешности по
правилу Рунге.
Модификации метода Эйлера.
Метод Эйлера обладает медленной сходимостью,
поэтому чаще применяют методы более высокого
порядка точности. Второй порядок точности по 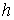 имеет усовершенствованный метод Эйлера :
имеет усовершенствованный метод Эйлера : 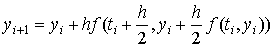 .
Этот метод имеет простую геометрическую
интерпретацию. Метод Эйлера называют методом
ломаных, так как интегральная кривая на
отрезке .
Этот метод имеет простую геометрическую
интерпретацию. Метод Эйлера называют методом
ломаных, так как интегральная кривая на
отрезке 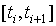 заменяется ломаной с угловым
коэффициентом заменяется ломаной с угловым
коэффициентом 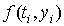 . В усовершенствованном методе
Эйлера интегральная кривая на отрезке . В усовершенствованном методе
Эйлера интегральная кривая на отрезке 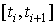 заменяется ломаной с угловым коэффициентом,
вычисленным в средней точке отрезка
заменяется ломаной с угловым коэффициентом,
вычисленным в средней точке отрезка 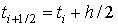 . Так как
значение . Так как
значение 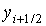 в этой точке неизвестно, для его
нахождения используют метод Эйлера с шагом в этой точке неизвестно, для его
нахождения используют метод Эйлера с шагом 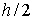 . .

ПРИМЕР 3. Решение задачи
усовершенствованным методом Эйлера.
Еще одна модификация метода Эйлера второго
порядка - метод Эйлера-Коши:
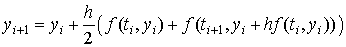
Решение систем дифференциальных
уравнений методом Эйлера.
Пусть требуется решить нормальную систему
дифференциальных уравнений:
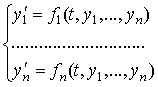
с начальными условиями: 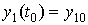 , , 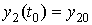 ,
..., ,
..., 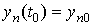
Эту систему в векторной форме можно записать в
виде: 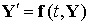 , , 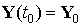 . Здесь . Здесь 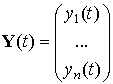 , , 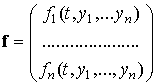 , , 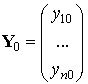 .
Расчетная формула метода Эйлера имеет вид: .
Расчетная формула метода Эйлера имеет вид: 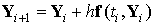 , , 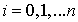 . .

|

