Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример
4 ~ Пример 5
Пример 1.
Найти все конечные особые точки функции 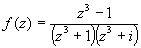 . .
Решение.
Поскольку числитель и знаменатель дроби -
аналитические функции, то особыми точками
являются нули знаменателя, т.е. корни уравнений 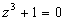 и и 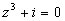 - шесть точек - шесть точек 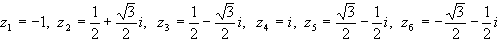 . .
Очевидно, что все эти точки изолированные и
являются полюсами, т.к. для каждой из них
справедливо 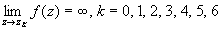 . .

Пример 2. Найти все конечные особые точки функции 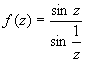 и определить их тип. и определить их тип.
Решение.
Поскольку числитель аналитическая функция, то
особыми точками f(z) являются точка z0
=0 и нули знаменателя - точки zk , для
которых
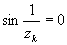 , ,
т.е. 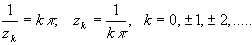 . .
Точки 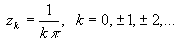
очевидно, изолированные особые точки. Это полюсы,
т.к. для каждой из них справедливо
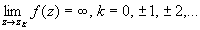
Точка z0 =0 не является изолированной
особой точкое, т.к. в любой ее окрестности, кроме
нее самой содержится бесконечное множество
особых точек - точек
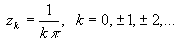
Такая особая точка называется предельной
особой точкой полюсов zk , ибо 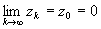 . .

Пример 3.
Определить тип особой точки z = 0 для функции 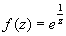 . .
Решение.
Точка z = 0 изолированная особая точка.
Поскольку 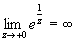 и и 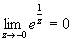 ,
т.е. не существует предел ,
т.е. не существует предел 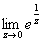 в действительной области (z = x), то он не
существует и в комплексной области, а это значит,
что точка z = 0 - существенно особая точка
функции
в действительной области (z = x), то он не
существует и в комплексной области, а это значит,
что точка z = 0 - существенно особая точка
функции 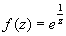 . .

Пример 4. Найти особые точки функции 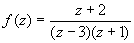 и определить их тип.
и определить их тип.
Решение.
Поскольку числитель и знаменатель дроби -
аналитические функции, то особыми точками
являются нули знаменателя - точки z = 3 и z =
-1.
Обе эти точки - простые нули знаменателя, т.е.
они являются простыми полюсами функции f(z).

Пример 5. Найти особые точки функции 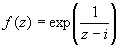 и
определить их тип. и
определить их тип.
Решение.
Единственная особая точка функции -
изолированная точка z = i.
Запишем (используя стандартное разложениедля
экспоненты) разложение функции в ряд Лорана по
степеням z - i:
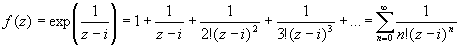
Главная часть полученного разложения содержит
бесконечное число членов, следовательно что
точка z = i - существенно особая.

|

