Изолированная
особая точка ~ Устранимая особая точка ~
Полюс ~ Существенно особая
точка ~ Порядок полюса
Точка z0, принадлежащая
области комплексных чисел, называется
изолированной особой точкой функции f(z),
если 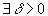 такая, что f(z) является
однозначной аналитической функцией в такая, что f(z) является
однозначной аналитической функцией в 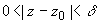 (в
самой точке аналитичность f(z) нарушается). (в
самой точке аналитичность f(z) нарушается).
Изолированная особая точка z0 функции f(z)
называется:
- устранимой особой точкой, если
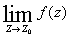 существует
и конечен; существует
и конечен;
- полюсом, если
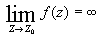 ; ;
- существенно особой точкой, если
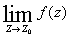 не
существует. не
существует.
ПРИМЕР 1. Отыскание особых точек рациональной
дроби.
ПРИМЕР 2. Определение типа
особых точек.
ПРИМЕР 3. Определение типа особой точки.
Для того чтобы особая точка функции f(z)
была ее устранимой особой точкой,
необходимо и достаточно, чтобы в разложении
функции в ряд Лорана в окрестности этой точки
отсутствовала главная часть. Это означает, что
если z0 - устранимая особая точка, то ряд
Лорана функции f(z) имеет вид: 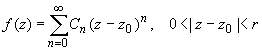 (1) (1)
для z0 - конечной точки, принадлежащей
области комплексных чисел.
Для того чтобы особая точка функции была полюсом,
необходимо и достаточно, чтобы главная часть
ряда Лорана функции в окрестности этой точки
содержала конечное число членов.
Ряд Лорана функции f(z) в случае z0-полюс
имеет вид:
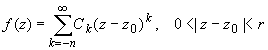 (2)
(2)
если z0 принадлежит области комплексных
чисел.
Номер старшего члена главной части ряда Лорана
функции в ее разложении в окрестности полюса
называется порядком полюса.
Так, точка z0 является полюсом порядка n
функции f(z), если в разложении (2) 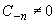 , Ck
= 0 при k < -n. , Ck
= 0 при k < -n.
Для того чтобы особая точка функции была ее существенно особой точкой, необходимо и
достаточно, чтобы главная часть ряда Лорана
функции в окрестности этой точки содержала
бесконечное число членов. Ряд Лорана функции f(z)
в случае z0 - существенно особой точки
имеет вид: 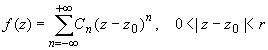 (3) (3)
если z0 принадлежит области комплексных
чисел.
ПРИМЕР 4. Определение типа
особых точек рациональной дроби.
ПРИМЕР 5. Определение типа
особых точек по Лорановскому разложению.

|

