Вертикальные
и наклонные асимптоты ~ Исследование
функций с помощью производной ~ Исследование
функций с помощью второй производной
Вертикальные и наклонные асимптоты.
Рассмотрим функцию 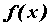 , определенную на
промежутке , определенную на
промежутке 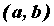 (возможно, (возможно, 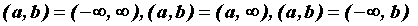 ) . Характер поведения
функции в области определения можно исследовать,
опираясь на следующие утверждения. ) . Характер поведения
функции в области определения можно исследовать,
опираясь на следующие утверждения.
Если 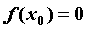 ,
то график функции пересекает ось абсцисс в точке ,
то график функции пересекает ось абсцисс в точке 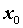 . .
Если 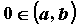 ,
то график функции пересекает ось ординат в
точке ,
то график функции пересекает ось ординат в
точке 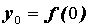 . .
Если в точке 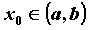 функция имеет бесконечный разрыв, то график
функции имеет вертикальную асимптоту функция имеет бесконечный разрыв, то график
функции имеет вертикальную асимптоту 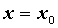 (Если
расстояние от точки кривой до некоторой
определенной прямой по мере удаления точки в
бесконечность стремится
к нулю, то эта прямая называется асимптотой
кривой. В случае бесконечного разрыва
расстояние от кривой до вертикальной асимптоты (Если
расстояние от точки кривой до некоторой
определенной прямой по мере удаления точки в
бесконечность стремится
к нулю, то эта прямая называется асимптотой
кривой. В случае бесконечного разрыва
расстояние от кривой до вертикальной асимптоты 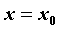 стремится к нулю при
стремится к нулю при 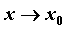 справа, слева или с
обеих сторон). справа, слева или с
обеих сторон).
Если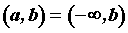 , , 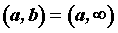 или или 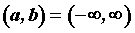 , существуют и конечны пределы , существуют и конечны пределы 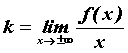 и и 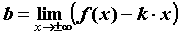 , то
прямая , то
прямая 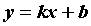 — асимптота графика функции. — асимптота графика функции.
Если 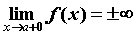 , то график функции имеет на левой
границе области сходимости вертикальную
асимптоту , то график функции имеет на левой
границе области сходимости вертикальную
асимптоту 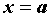 ; аналогично, если ; аналогично, если 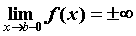 , то график функции
имеет на правой границе области сходимости
вертикальную асимптоту , то график функции
имеет на правой границе области сходимости
вертикальную асимптоту 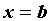 . .
Если 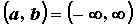 и существует такое число и существует такое число 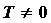 , что , что 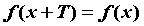 для
любого для
любого 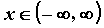 , то исследуемая функция периодична с
периодом , то исследуемая функция периодична с
периодом 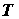 ; в этом случае достаточно построить
график функции на промежутке ; в этом случае достаточно построить
график функции на промежутке 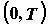 и доопределить его по
периодичности на всю числовую ось. и доопределить его по
периодичности на всю числовую ось.
Если 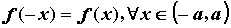 , то исследуемая функция четная; этом
случае график симметричен относительно оси
ординат; достаточно построить график функции на
промежутке , то исследуемая функция четная; этом
случае график симметричен относительно оси
ординат; достаточно построить график функции на
промежутке 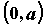 и отобразить его симметрично
относительно оси ординат на и отобразить его симметрично
относительно оси ординат на 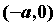 . .
Если 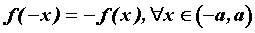 , то исследуемая функция нечетная; этом
случае график симметричен относительно начала
координат; достаточно построить график функции
на промежутке , то исследуемая функция нечетная; этом
случае график симметричен относительно начала
координат; достаточно построить график функции
на промежутке 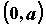 и отобразить его симметрично
относительно начала координат на и отобразить его симметрично
относительно начала координат на 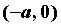 . .
ПРИМЕР 1 . Отыскание асимптот
графика функции.
Исследование функций с помощью
производной.
Если функция дифференцируема
на промежутке 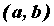 , за исключением, быть может, конечного
числа точек этого промежутка, то можно дополнить
изучение поведения функции исследованием на экстремум
(точки максимума и точки минимума функции
имеют общее название — точки экстремума),
используя следующие утверждения. , за исключением, быть может, конечного
числа точек этого промежутка, то можно дополнить
изучение поведения функции исследованием на экстремум
(точки максимума и точки минимума функции
имеют общее название — точки экстремума),
используя следующие утверждения.
Для того, чтобы дифференцируемая на 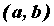 функция
не убывала (не возрастала) на этом промежутке,
необходимо и достаточно, чтобы функция
не убывала (не возрастала) на этом промежутке,
необходимо и достаточно, чтобы 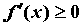 ( (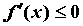 ) на ) на 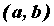 . .
Пусть в точке 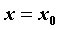 производная производная
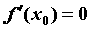 или
не существует. Если существует окрестность точки или
не существует. Если существует окрестность точки
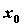 ,
такая, что для ,
такая, что для 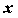 из этой окрестности из этой окрестности 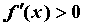 при при 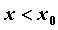 и и 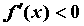 при при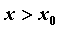 , то функция имеет в
точке , то функция имеет в
точке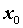 максимум. Если же
максимум. Если же 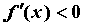 при при 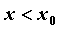 и и 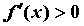 при при 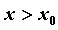 , то функция имеет в
точке , то функция имеет в
точке 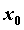 минимум (в этом случае говорят, что “производная
меняет знак при переходе через точку
минимум (в этом случае говорят, что “производная
меняет знак при переходе через точку 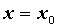 ”). ”).
Если непрерывная в точке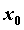 функция функция 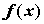 дифференцируема
на дифференцируема
на 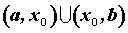 ,
при этом ,
при этом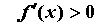 на на 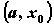 и и 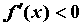 на на 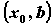 , то функция имеет в точке , то функция имеет в точке 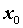 максимум;
если же максимум;
если же 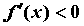 при при 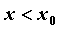 и и 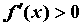 при при 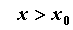 , то функция имеет в точке , то функция имеет в точке 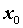 минимум.
минимум.
ПРИМЕР 2 . Нахождение интервалов
монотонности и экстремумов.
Исследование функций с помощью второй
производной.
Если функция дважды дифференцируема на
промежутке 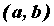 , за исключением, быть может, конечного
числа точек этого промежутка, то исследование
поведения функции можно дополнить исследованием
выпуклости и вогнутости. , за исключением, быть может, конечного
числа точек этого промежутка, то исследование
поведения функции можно дополнить исследованием
выпуклости и вогнутости.
График функции 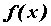 называется выпуклым
(выпуклым вниз) на промежутке называется выпуклым
(выпуклым вниз) на промежутке 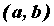 , если он расположен
выше касательной, проведенной в любой точке , если он расположен
выше касательной, проведенной в любой точке 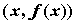 , , 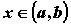 . Если
же график функции лежит ниже касательной, — то он называется
вогнутым (выпуклым вверх). . Если
же график функции лежит ниже касательной, — то он называется
вогнутым (выпуклым вверх).
Если дважды дифференцируемая на промежутке 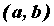 функция функция
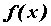 имеет
на нем положительную вторую производную, то
функция выпуклая на имеет
на нем положительную вторую производную, то
функция выпуклая на 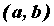 . Если же вторая
производная отрицательна на промежутке . Если же вторая
производная отрицательна на промежутке 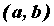 , то
функция на нем вогнута. , то
функция на нем вогнута.
Если вторая производная равна нулю в точке 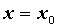 , а слева
и справа от нее имеет значения разных знаков,
точка , а слева
и справа от нее имеет значения разных знаков,
точка 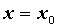 — точка перегиба.
— точка перегиба.
ПРИМЕР 3 . Нахождение интервалов
выпуклости, вогнутости и точек перегиба.

|

