Непрерывность
и разрывы функции ~ Односторонние
пределы функции в точке ~ Классификация
разрывов
Непрерывность и разрывы функции.
Рассмотрим функцию 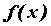 , определенную на некотором промежутке , определенную на некотором промежутке 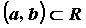 .
Функция .
Функция 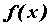 непрерывна в точке непрерывна в точке 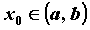 , если предел функции в точке , если предел функции в точке 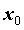 равен
значению функции в этой точке, равен
значению функции в этой точке, 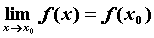 . .
ПРИМЕР 1 . Доказательство
непрерывности функции в точке
Односторонние пределы функции в точке.
Функция, непрерывная в каждой точке промежутка 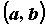 ,
называется непрерывной на промежутке. Если
функция ,
называется непрерывной на промежутке. Если
функция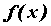 определена на промежутке определена на промежутке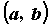 , , 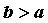 , то при
исследовании поведения функции , то при
исследовании поведения функции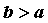 в окрестности точки в окрестности точки 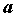 имеет смысл говорить
о пределе функции в точке имеет смысл говорить
о пределе функции в точке 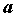 справа, а при
исследовании в окрестности точки справа, а при
исследовании в окрестности точки 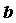 - о
пределе функции в точке - о
пределе функции в точке 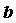 слева. Число слева. Число 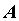 называется пределом справа функции
называется пределом справа функции 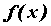 при при 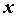 , стремящемся к , стремящемся к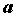 , если для любого
положительного числа , если для любого
положительного числа 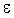 , как бы мало оно ни
было, существует такое положительное число , как бы мало оно ни
было, существует такое положительное число 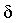 , что
для всех , что
для всех 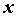 ,
удовлетворяющих неравенству ,
удовлетворяющих неравенству 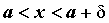 , справедливо
неравенство , справедливо
неравенство 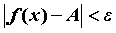 . Говорят “предел справа функции в
точке . Говорят “предел справа функции в
точке 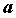 ”
и обозначают ”
и обозначают 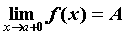 . Аналогично говорят “предел слева
функции . Аналогично говорят “предел слева
функции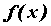 в точке в точке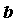 ” и
обозначают ” и
обозначают 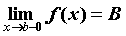 , если для любого положительного числа , если для любого положительного числа 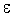 , как бы
мало оно ни было, существует такое положительное
число , как бы
мало оно ни было, существует такое положительное
число 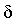 ,
что для всех ,
что для всех 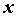 ,
удовлетворяющих неравенству ,
удовлетворяющих неравенству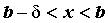 , справедливо
неравенство , справедливо
неравенство 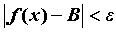 . Для существования предела функции в
точке, необходимо и достаточно, чтобы
существовали и совпадали односторонние пределы
функции в этой точке. По той же схеме вводится
понятие непрерывности слева и непрерывности
справа. Функция . Для существования предела функции в
точке, необходимо и достаточно, чтобы
существовали и совпадали односторонние пределы
функции в этой точке. По той же схеме вводится
понятие непрерывности слева и непрерывности
справа. Функция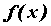 ,
определенная на отрезке ,
определенная на отрезке 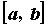 , , 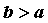 , непрерывна справа в
точке , непрерывна справа в
точке 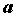 , если , если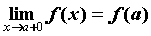 и
непрерывна слева в точке и
непрерывна слева в точке 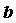 , если , если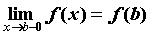 . Для того чтобы
функция была непрерывна в точке . Для того чтобы
функция была непрерывна в точке 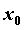 необходимо и достаточно, чтобы
односторонние пределы функции в точке совпадали
со значением функции в этой точке: необходимо и достаточно, чтобы
односторонние пределы функции в точке совпадали
со значением функции в этой точке: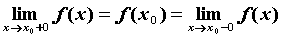 . Если
хотя бы одно из равенств нарушается, говорят о
разрыве в точке . Если
хотя бы одно из равенств нарушается, говорят о
разрыве в точке 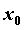 . .
ПРИМЕР 2 . Вычисление
односторонних пределов
Классификация разрывов.
Если хотя бы одно из равенств 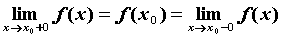 нарушается, говорят о
разрыве в точке нарушается, говорят о
разрыве в точке 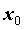 . Если . Если 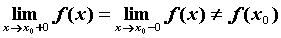 и односторонние
пределы конечны, то разрыв в точке и односторонние
пределы конечны, то разрыв в точке 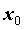 называется
устранимым. Если называется
устранимым. Если 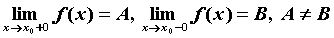 и оба односторонние
пределы конечны, то говорят о скачке функции
в точке и оба односторонние
пределы конечны, то говорят о скачке функции
в точке 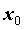 . Устранимый разрыв и скачок называются
разрывами первого рода. Если один из
односторонних пределов бесконечен или не
существует, то разрыв называется разрывом
второго рода. Так же, как для предела и
непрерывности, говорят о разрыве слева и разрыве
справа. . Устранимый разрыв и скачок называются
разрывами первого рода. Если один из
односторонних пределов бесконечен или не
существует, то разрыв называется разрывом
второго рода. Так же, как для предела и
непрерывности, говорят о разрыве слева и разрыве
справа.
ПРИМЕР 3 . Определение типа
точки разрыва

|

