Синтаксис:

            z = fzero(‘<имя функции>‘, x0)
            z = fzero(‘<имя функции>‘, x0, tol)
            z = fzero(‘<имя функции>‘, x0, tol, trace)

Описание:

Функция z = fzero(‘<имя функции>‘, x0) находит нуль функции в окрестности точки x0.

Функция z = fzero(‘<имя функции>‘, x0, tol) возвращает результат с относительной погрешностью tol, задаваемой пользователем. По умолчанию tol = eps.

Функция z = fzero(‘<имя функции>‘, x0, tol, trace) позволяет выдавать на экран терминала промежуточные результаты поиска нуля функции.

Пример:

Вычислим действительные нули полинома f(x) = x⁴ - 4 * x³ + 12.

Сначала сформируем М-файл polynom4 для вычисления этой функции:

            function y = polynom4(x)
            y = x.^4 - 4*x.^3 + 12;

затем найдем корень полинома, стартуя из точки x0 = -0.5:

            z = fzero(' polynom4', -0.5, eps, 1)
            z = 1.746170944975038e+000;

теперь найдем корень полинома, стартуя из точки x0 = 3.0:

            z = fzero(' polynom4', 3, eps, 1)
            z = 3.777351952771215e+000;

точные значения корней полинома могут быть вычислены с помощью функции

            roots([1 -4 0 0 12])
            ans =

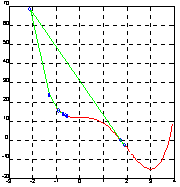
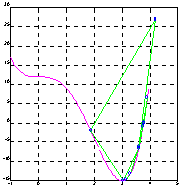
Нетрудно видеть, что оба подхода обеспечивают согласованные результаты.

На рис. а показана траектория движения из точки x0 = -0.5, а на рис. б - из точки x0 = 3.0.

а)	б)

Алгоритм:

Функция fzero использует методы деления отрезка пополам, секущей и обратной квадратической интерполяции [1, 2].

Сопутствующие функции: FMIN, ROOTS.

Ссылки:

1. Brent R. Algorithms for Minimization Without Derivatives. Prentice-Hall, 1973.

2. Forsythe G. E., Malcolm M. A., Moler C. B. Computer Methods for Mathematical Computations. Prentice-Hall, 1976.