Синтаксис:

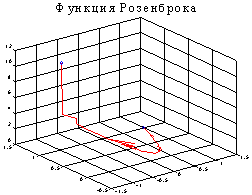
            xmin = fmins(‘<имя функции>‘, x0)
            xmin = fmins(‘<имя функции>‘, x0, options)
            [xmin, options] = fmins(‘<имя функции>‘, x0, options, [ ], arg1,..., arg10)

Описание:

Функция xmin = fmins(‘<имя функции>‘, x0) возвращает вектор xmin, соответствующий значению локального минимума функции в окрестности точки x0.

Функция xmin = fmins(‘<имя функции>‘, x0, options) использует вектор управляющих параметров options, который включает 18 компонентов, соответствующих функции foptions. Функция fmins использует только 4 из этих параметров: options(1), options(2), options(3), options(14).

Функция [xmin, options] = fmins(‘<имя функции>‘, x0, options, [ ], arg1,..., arg10) позволяет передать до 10 параметров; четвертый входной аргумент необходим, чтобы обеспечить совместимость с функцией fminu из пакета Optimization Toolbox [1]. Кроме того, возвращается вектор управляющих параметров options, которые использовались алгоритмом, и в частности, параметр options(10), фиксирующий количество выполненных итераций, и параметр options(8), содержащий минимальное значение функции.

Пример:

Рассмотрим классический пример минимизации функции Розенброка от двух переменных.

          .

Минимум этой функции достигается в точке (a, a²) и равен нулю. В качестве начальной точки обычно выбирается точка (-1.2 1).

Определим М-файл rosenbr(x, a), обеспечивающий вычисление этой функции для заданного параметра a.

           function y = rosenbr(x, a)
           if nargin < 2, a = 1; end
           y = 100 * (x(2) - x(1)^2)^2 + (a - x(1))^2;

Рассмотрим случай a = 1.

          [xmin, opt] = fmins('rosenbr', [-1.2 1], [0, 1e-6]);
          xmin = 9.999997969915502e-001      9.999995750683192e-001

Анализ таблицы подтверждает, что заданная итерационная погрешность opt(2) равна 1.0000e-06; минимальное значение функции opt(8) равно 7.6989e-014; число выполненных итераций opt(10) равно 1.9900e+002 при максимально допустимом числе итераций opt(14) = 4.0000e+002.

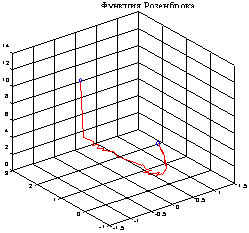
Рассмотрим случай, когда минимум сдвинут в точку (sqrt(2), 2).

            [xmin, opt] = fmins('rosenbr', [-1.2 1], [0, 1e-6], [ ], sqrt(2));
            xmin, opt(8), opt(10)
            xmin = 1.414213634743838e+000     2.000000234240279e+000
            opt(8) = 9.2528e-014
            opt(10) = 206

Алгоритм:

Функция fmins реализует метод Нелдера - Мида [2, 3], который является прямым методом, не требующим вычисления градиента или иной информации о производной, и связан с построением симплекса в n-мерном пространстве, который задается n+1-й вершиной. В двумерном пространстве симплекс - это треугольник, а в трехмерном - пирамида.

На каждом шагу алгоритма новая точка выбирается внутри или вблизи симплекса. Значение функции в этой точке сравнивается со значениями в вершинах симплекса, и, как правило, одна из вершин заменяется этой точкой, задавая тем самым новый симплекс. Эти итерации повторяются до тех пор, пока диаметр симплекса не станет меньше заданной величины итерационной погрешности по переменным x.

Сопутствующие функции: FMIN, FZERO, Optimization Toolbox.

Ссылки:

1. Optimization Toolbox. User’s Guide. Natick: The MathWorks, Inc., 1991.

2. Nelder J. A., Mead R. A Simplex Method for Function Minimization//Computer Journal. Vol. 7, P. 308-313.

3. Dennis J. E., Woods D. J. New Computing Environments: Microcomputers in Large-Scale Computing, Ed. by A. Wouk. SIAM, 1987. P. 116-122.