|
![[Graphics:Images/index_gr_1.gif]](Images/index_gr_1.gif)
Рассматриваемя здесь схема содержит
туннельный диод, подключенный через резистор Rs к
источнику постоянного или изменяющегося
напряжения Es. Значения Es и Rs задают исходную
точку устройства на N-образной аольтамперной
характеристике ВАХ туннельного диода. От выбора
этой точки и параметров реактивных элементов
(индуктивности L и емкости C) зависит режим работы
цепи. Ниже рассмотрены основные режимы работы
цепи с туннельным диодом, что дает представление
о больших функциональных возможностях подобных
схем.
Поведение данной схемы при Es=const
описывается системой дифференциальных
уравнений, приведенных ниже:
di (t) /dt = (Es-i (t) Rs-u (t)) /L
du (t) /dt = (i (t) -I (u)) /C
Эта система нелинейна вследствии
нелинейности зависимости I(u) у туннельного диода,
задаваемой его N-образной вольтамперной
характеристикой. Мы будем использовать для
решения этой нелинейной системы встроенную
функцию системы Mathematica 4 NDSolve. Она позволяет
найти решение указанной выше системы в виде
временных зависимостей тока i (t) в цепи RsL и
напряжения u (t) на туннельном диоде. Решение
находится при начальных условиях i (0) =0 и (0) =0,
начиная с момента времени е=0. Для наглядности
решение представляется также в фиде фазового
портрета - совокупности значений i(t) и u(t) на
фазовой плоскости, на которой строятся также ВАХ
туннельного диода и линия нагрузки резистора R.
Это дает максимально наглядное представление о
работе схемы.
Для придания описываемой модели
универсальности будем считать, что ВАХ задана
таблицей значений U и I, представленных списком:
![[Graphics:Images/index_gr_2.gif]](Images/index_gr_2.gif)
Это позволяет не меняя методики
моделирования цепи задавать любые N-образные ВАХ.
Однако, для моделирования нужно иметь
непрерывную ВАХ. Воспользуемся для этого
полиномиальной интерполяцией, выполняемой с
помощью встроенной функции Interpolation при степени
полинома, равной 4:
![[Graphics:Images/index_gr_3.gif]](Images/index_gr_3.gif)
Построим график вольтамперной
характеристики:
![[Graphics:Images/index_gr_4.gif]](Images/index_gr_4.gif)
![[Graphics:Images/index_gr_5.gif]](Images/index_gr_5.gif)
![[Graphics:Images/index_gr_6.gif]](Images/index_gr_6.gif)
Теперь рассмотрим осеновные
случаи работы
В этом случае рабочая точка пересечения
ВАХ I(U) с линией нагрузки является единственной и
устойчива.Зададим параметры цепи и найдем
решение системы дифференциальных уравнений - оно
размещавется в векторе R.
![[Graphics:Images/index_gr_7.gif]](Images/index_gr_7.gif)
![[Graphics:Images/index_gr_8.gif]](Images/index_gr_8.gif)
![[Graphics:Images/index_gr_9.gif]](Images/index_gr_9.gif)
Построим графики временных
зависимостей решения (напряжения Es(t),
напряжения u(t) и тока i(t)):
![[Graphics:Images/index_gr_10.gif]](Images/index_gr_10.gif)
![[Graphics:Images/index_gr_11.gif]](Images/index_gr_11.gif)
![[Graphics:Images/index_gr_12.gif]](Images/index_gr_12.gif)
![[Graphics:Images/index_gr_13.gif]](Images/index_gr_13.gif)
Эти графики описывают затухащий
колебательный процесс.
Для повышения наглядности развития
процессов в схеме зададим решение еще в одной
форме - фазового портрета на фоне N-образной ВАХ:
![[Graphics:Images/index_gr_14.gif]](Images/index_gr_14.gif)
![[Graphics:Images/index_gr_15.gif]](Images/index_gr_15.gif)
![[Graphics:Images/index_gr_16.gif]](Images/index_gr_16.gif)
![[Graphics:Images/index_gr_17.gif]](Images/index_gr_17.gif)
Фазовый портрет имеет вид спирали,
которая скручивается вокруг точки пересенчения
ВАХ линией нагрузки. Такой режим характерен для
применения цепи в режиме усиления синусоилалов.
Следующий случай показывает
возможность применения цепи для создания
генераторов синусоидальных колебаний с частотой
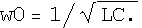
![[Graphics:Images/index_gr_19.gif]](Images/index_gr_19.gif)
![[Graphics:Images/index_gr_20.gif]](Images/index_gr_20.gif)
![[Graphics:Images/index_gr_21.gif]](Images/index_gr_21.gif)
![[Graphics:Images/index_gr_22.gif]](Images/index_gr_22.gif)
![[Graphics:Images/index_gr_23.gif]](Images/index_gr_23.gif)
![[Graphics:Images/index_gr_24.gif]](Images/index_gr_24.gif)
![[Graphics:Images/index_gr_25.gif]](Images/index_gr_25.gif)
![[Graphics:Images/index_gr_26.gif]](Images/index_gr_26.gif)
В данном случае спираль фазового
портрета закручивается в стационарный эллипс.
![[Graphics:Images/index_gr_27.gif]](Images/index_gr_27.gif)
Релаксационные колебания возникают,
когда индуктивность возрастает, а емкоть C
уменьшается. Этот случай показан нижек.
![[Graphics:Images/index_gr_28.gif]](Images/index_gr_28.gif)
![[Graphics:Images/index_gr_29.gif]](Images/index_gr_29.gif)
![[Graphics:Images/index_gr_30.gif]](Images/index_gr_30.gif)
![[Graphics:Images/index_gr_31.gif]](Images/index_gr_31.gif)
![[Graphics:Images/index_gr_32.gif]](Images/index_gr_32.gif)
Форма колебаний заметно отлична
от синусоидальной, что объясняется заметной
индуктивностью L и емкостью цепи.
![[Graphics:Images/index_gr_33.gif]](Images/index_gr_33.gif)
![[Graphics:Images/index_gr_34.gif]](Images/index_gr_34.gif)
![[Graphics:Images/index_gr_35.gif]](Images/index_gr_35.gif)
![[Graphics:Images/index_gr_36.gif]](Images/index_gr_36.gif)
![[Graphics:Images/index_gr_37.gif]](Images/index_gr_37.gif)
![[Graphics:Images/index_gr_38.gif]](Images/index_gr_38.gif)
![[Graphics:Images/index_gr_39.gif]](Images/index_gr_39.gif)
![[Graphics:Images/index_gr_40.gif]](Images/index_gr_40.gif)
![[Graphics:Images/index_gr_41.gif]](Images/index_gr_41.gif)
![[Graphics:Images/index_gr_42.gif]](Images/index_gr_42.gif)
![[Graphics:Images/index_gr_43.gif]](Images/index_gr_43.gif)
![[Graphics:Images/index_gr_44.gif]](Images/index_gr_44.gif)
![[Graphics:Images/index_gr_45.gif]](Images/index_gr_45.gif)
![[Graphics:Images/index_gr_46.gif]](Images/index_gr_46.gif)
![[Graphics:Images/index_gr_47.gif]](Images/index_gr_47.gif)
![[Graphics:Images/index_gr_48.gif]](Images/index_gr_48.gif)
![[Graphics:Images/index_gr_49.gif]](Images/index_gr_49.gif)
![[Graphics:Images/index_gr_50.gif]](Images/index_gr_50.gif)
![[Graphics:Images/index_gr_51.gif]](Images/index_gr_51.gif)
![[Graphics:Images/index_gr_52.gif]](Images/index_gr_52.gif)
![[Graphics:Images/index_gr_53.gif]](Images/index_gr_53.gif)
![[Graphics:Images/index_gr_54.gif]](Images/index_gr_54.gif)
![[Graphics:Images/index_gr_55.gif]](Images/index_gr_55.gif)
![[Graphics:Images/index_gr_56.gif]](Images/index_gr_56.gif)
![[Graphics:Images/index_gr_57.gif]](Images/index_gr_57.gif)
![[Graphics:Images/index_gr_58.gif]](Images/index_gr_58.gif)
![[Graphics:Images/index_gr_59.gif]](Images/index_gr_59.gif)
![[Graphics:Images/index_gr_60.gif]](Images/index_gr_60.gif)
![[Graphics:Images/index_gr_61.gif]](Images/index_gr_61.gif)
![[Graphics:Images/index_gr_62.gif]](Images/index_gr_62.gif)
![[Graphics:Images/index_gr_63.gif]](Images/index_gr_63.gif)
![[Graphics:Images/index_gr_64.gif]](Images/index_gr_64.gif)
![[Graphics:Images/index_gr_65.gif]](Images/index_gr_65.gif)
![[Graphics:Images/index_gr_66.gif]](Images/index_gr_66.gif)
Для этого случая рабочая точка выбрана
вблизи максимума ВАХ и расположена на восходящем
участке ее. Периодический синусоидальный сигнал
выводит ее на падающий участок.
![[Graphics:Images/index_gr_67.gif]](Images/index_gr_67.gif)
![[Graphics:Images/index_gr_68.gif]](Images/index_gr_68.gif)
![[Graphics:Images/index_gr_69.gif]](Images/index_gr_69.gif)
![[Graphics:Images/index_gr_70.gif]](Images/index_gr_70.gif)
![[Graphics:Images/index_gr_71.gif]](Images/index_gr_71.gif)
![[Graphics:Images/index_gr_72.gif]](Images/index_gr_72.gif)
![[Graphics:Images/index_gr_73.gif]](Images/index_gr_73.gif)
![[Graphics:Images/index_gr_74.gif]](Images/index_gr_74.gif)
![[Graphics:Images/index_gr_75.gif]](Images/index_gr_75.gif)
![[Graphics:Images/index_gr_76.gif]](Images/index_gr_76.gif)
Цепь может работать в триггерном режиме,
т. е. иметь два состояния равновесия, переход в
которые осуществляется наложением на Es
импульсов положительной и отрицательной
полярности. Линия нагрузки должна в этом случае
пересекать ВАХ в двух точках, расположенных на
восходящих участках ВАХ. Для моделирования
создадим нужную временную зависимость источника
питания Es(t)=e(t):
![[Graphics:Images/index_gr_77.gif]](Images/index_gr_77.gif)
![[Graphics:Images/index_gr_78.gif]](Images/index_gr_78.gif)
Ниже представлен рассчет
переходных просессов в данной схеме:
![[Graphics:Images/index_gr_79.gif]](Images/index_gr_79.gif)
![[Graphics:Images/index_gr_80.gif]](Images/index_gr_80.gif)
![[Graphics:Images/index_gr_81.gif]](Images/index_gr_81.gif)
![[Graphics:Images/index_gr_82.gif]](Images/index_gr_82.gif)
![[Graphics:Images/index_gr_83.gif]](Images/index_gr_83.gif)
![[Graphics:Images/index_gr_84.gif]](Images/index_gr_84.gif)
![[Graphics:Images/index_gr_85.gif]](Images/index_gr_85.gif)
![[Graphics:Images/index_gr_86.gif]](Images/index_gr_86.gif)
![[Graphics:Images/index_gr_87.gif]](Images/index_gr_87.gif)

|

