  В
этом разделе обсуждается, как в символьном виде
решать уравнения и системы уравнений. Команда Решить
относительно переменной из меню Символика
позволяет решить уравнение относительно
некоторой переменной и выразить его корни через
остальные параметры уравнения.
В этом разделе описывается также, как в
символьном виде решить систему уравнений,
используя блоки решения уравнений. Для этого
требуется Mathcad PLUS.
Решать уравнение символьно гораздо труднее,
чем численно. Может оказаться, что в символьном
виде решение не существует. Это может быть
вызвано рядом причин, обсуждаемых в разделе “Ограничения символьных
преобразований”.
Решение уравнения относительно переменной
Чтобы решить уравнение относительно
переменной:
- Напечайте уравнение. Убедитесь, что для
выведения знака равенства использована
комбинация клавиш [Ctrl]=.
- Выделите переменную, относительно которой
нужно решить уравнение, щёлкнув на ней мышью.
- Выберите Решить относительно переменной из
меню Символика
Mathcad решит уравнение относительно выделенной
переменной и вставит результат в рабочий
документ. Обратите внимание, что, если переменная
возводилась в квадрат в первоначальном
уравнении, при решении можно получить два ответа.
Mathcad отображает их в виде вектора. Рисунок 20
показывает соответствующий пример.

Рисунок 20: Преобразование выражения для
решения уравнения.
Можно также решать неравенство, использующее
символы <, >, 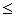 и и 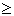 . Решения для неравенств будут отображаться в
терминах булевых выражений Mathcad. Если имеется
более одного решения, Mathcad помещает их в вектор. В
Mathcad булево выражение типа x < 2 имеет
значение 1, если оно истинно, и 0, — если оно ложно.
Таким образом, решение “x — меньше, чем 2, и
больше, чем -2”, можно было бы представить
выражением (x < 2)
. Решения для неравенств будут отображаться в
терминах булевых выражений Mathcad. Если имеется
более одного решения, Mathcad помещает их в вектор. В
Mathcad булево выражение типа x < 2 имеет
значение 1, если оно истинно, и 0, — если оно ложно.
Таким образом, решение “x — меньше, чем 2, и
больше, чем -2”, можно было бы представить
выражением (x < 2) (-2 < x). (-2 < x).
Нахождение корней уравнения
Процедура нахождения корней уравнения
аналогична более общей проблеме решения
уравнения относительно некоторой переменной.
Чтобы найти корни выражения, надо:
- Напечатать выражение.
- Выделить в любом месте переменную, относительно
которой уравнение решается.
- Выбрать пункт Решить относительно переменной
из меню Символика.
Обратите внимание, что нет никакой
необходимости приравнивать выражение нулю. Если
Mathcad не находит знака равенства, он предполагает,
что требуется приравнять выражение нулю.

Рисунок 21: Примеры нахождения корней и решения
неравенств.

Рисунок 22: Некоторые примеры использования
символьного решения.
Символьное решение системы уравнений
В Главе “Решение
уравнений” рассказывается, как
использовать блоки решения уравнений, чтобы
решить систему уравнений. Использование функции Find
даёт численные значения для неизвестных в
системе уравнений. Если Вы используете Mathcad PLUS,
можно подобным образом находить решения систем
уравнений в символьном виде.
Чтобы решить систему уравнений в символьном
виде, необходимо выполнить следующее:
- Напечатайте слово Given. Это сообщает Mathcad, что
далее следует система уравнений. Можно
напечатать Given в любой комбинации символов
верхнего и нижнего регистра и в любом шрифте.
Убедитесь только, что Вы не печатаете его в
текстовой области или параграфе.
- Теперь напечатайте уравнения в любом порядке
ниже слова Given. Удостоверьтесь, что для ввода
знака = используется [Ctrl]=.
- Напечатайте функцию Find, соответствующую
системе уравнений. Аргументами функции являются
переменные, относительно которых система
решается.
- Нажмите [Ctrl]. (клавиша CTRL,
сопровождаемая точкой). Mathcad отображает
символьный знак равенства.
- Щёлкните мышью на функции Find.
Mathcad отображает решения для системы уравнений
справа от стрелки. Если функция Find имеет один
аргумент, Mathcad возвращает один результат. Если Find
имеет более одного аргумента, Mathcad возвращает
вектор результатов. Например, Find(x, y)
возвращает вектор, содержащий выражения для x
и y , который является решением системы
уравнений. Обратите внимание, что, если система
является переопределенной нелинейной системой,
функция Find не будет возвращать решение.
Используйте в этом случае функцию Minerr вместо Find.
Minerr будет возвращать ответ, который минимизирует
невязку при заданных ограничениях.
Большинство рекомендаций для блоков решения
уравнений, приведенных в Главе “Решение уравнений”,
применяется к решению систем уравнений в
символьном виде. Основное различие заключается в
том, что при символьном решении не нужно вводить
начальные значения для решений.
Рисунок 23 показывает пример блока решения
уравнений, используемого для символьного
решения системы уравнений. Более подробно
относительно блоков решения уравнений, см. Главу
“Решение уравнений”.

Рисунок 23: Символьное решение системы
уравнений.
  
|

