  При
работе с символьным процессором несомненно
обнаружится, что:
- многие вычисления могут быть выполнены только
численно, и
- ещё больше вычислений возвращают такие длинные
ответы, что оказывается удобнее выполнять их
численно.
Для компьютера символьные операции, вообще
говоря, намного более трудны, чем
соответствующие численные операции. Очень
маловероятно, что для произвольной достаточно
сложной функции удастся выписать первообразную
через элементарные функции либо удастся найти
формулу корней уравнения, которое содержит такую
функцию. Много обманчиво просто смотрящихся
функций, сконструированных из элементарных
частей, подобных степеням и корням,
показательным функциям, логарифмам и
тригонометрическим функциям, не имеют
неопределённого интеграла, выражаемого через
элементарные функции.
Особенности символьной обработки
При использовании символьного решающего
устройства не забудьте, что символьное решение
очень отличается от численного. Символьное
решающее устройство может не найти решения, даже
если оно существует. Это происходит потому, что
много уравнений, которые могут легко быть решены
численно, не имеют точного символьного решения.
Например, не существует формулы, подобной
формуле для корней квадратного уравнения,
которая дает корни полинома степени 5 или выше.
Даже некоторые простые уравнения, подобные x=cos(x),
не могут быть решены в символьном виде. Когда
уравнение имеет несколько решений, Mathcad иногда
возвращает только одно из них и запрашивает, не
следует ли показать весь результат, находящийся
в буфере обмена. Если нажать“OK”, Mathcad показывает
вектор, содержащий найденные решения и слово Root.
В буфере обмена вместо слова Root находится
выражение вида “RootOf (функция от Z)”. Корни
функции RootOf совпадают с решениями исходного
уравнения. Как и для других символьных операций,
получаемые ответы зависят от того, содержат ли
константы в уравнении десятичные точки. Если
константы — рациональные числа подобно 1/2 или 4,
символьный процессор попытается найти точное
решение. Например, решение для первого
квадратного уравнения на Рисунке 21 является
точным; фактически это просто формула корней
квадратного уравнения. Но если напечатать .5
вместо 1/2, Mathcad вернёт приближенные числовые
значения
Длинные ответы
Символьные вычисления могут легко производить
настолько длинные ответы, что они не помещаются в
рабочем окне. Если ответ состоит из суммы
отдельных членов, можно переформатировать такой
ответ, используя оператор “Разбить плюсами”.
Чтобы разбить выражение на части знаками плюс,
необходимо:
- Выделить крайний левый член выражения.
- Нажать несколько раз [],
пока знак плюс не попадет на нужное место и
находящийся после него член не окажется в
выделяющей рамке.
- Нажать [Del]. Последний знак плюс в
выделяющей рамке будет заменен местом ввода
операнда.
- Затем напечатать [Ctrl][
 ], чтобы вставить
знак плюс с переносом. ], чтобы вставить
знак плюс с переносом.
Можно повторять этот процесс, пока имеются
отдельные члены, соединенные знаками плюс.
Иногда символьный ответ может быть настолько
длинным, что его не удаётся удобно отобразить в
рабочем документе. В этом случае Mathcad спросит, не
следует ли поместить ответ в буфер обмена.
Если нажать “OK”, Mathcad помещает строку,
представляющую ответ, в буфер обмена. Чтобы
увидеть эту строку, надо:
- Открыть группу Главная в окне Диспетчера
программ.
- Дважды щёлкнуть на иконке Окно Буфера Обмена.
Вы увидите ответ, написанный на
ФОРТРАНоподобном языке, как показано на Рисунке
30. Этот язык использует следующие соглашения:
- Символы +, -, *, и / означают основные
арифметические операции. Возведение в степень
обозначается **.
- Производная f(x) по x
записывается в виде . Производная n-ого
порядка — diff( f(x), x$n).
- D обозначает оператор частной производной.
Производная n-ного порядка — ( D, n). Частная
производная функции по n-ному аргументу — (
D[n]).
- Интеграл от f(x) по x выражается в
виде int( f(x), x).
- Операторы суммы и произведения обозначаются sum(
) и product( ).
- Оператор @ означает композицию функций.
Например, (sin@exp) (x) — то же самое, что sin (exp (x)). @@
представляет кратную композицию, так что ( f@@2) (x)
— то же самое, что f( f(x)).
- RootOf (уравнение) замещает любой корень
алгебраического уравнения. Например, RootOf (Z ** 2 + 1)
представляет или i или -i.
- Можно видеть внедренные коды шрифта (подобно
MFNT_03_) предшествующие именам переменных,
указывающие шрифт, на котором должно появиться
имя переменной.
Чтобы вставить ответ в виде текста в рабочий
документ Mathcad:
- Щёлкните мышью в свободном месте.
- Выберите Вставить из меню Правка.
Чтобы сохранить этот длинный ответ как
отдельный текстовый файл, выберите Сохранить
как... из меню Файл Буфера Обмена.
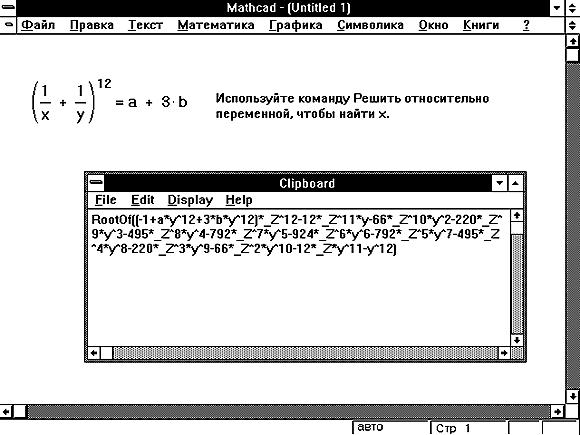
Рисунок 30: Длинный символьный ответ в буфере
обмена.
  
|

