  Оператор
интегрирования в Mathcad предназначен для
численного вычисления определенного интеграла
функции по некоторому интервалу.
Например, определенный интеграл sin(x)2 от 0
до p/4 может быть
вычислен следующим образом:
- Щёлкните в свободном месте и наберите знак &.
Появится знак интеграла с пустыми полями
для подинтегрального выражения, пределов
интегрирования и переменной
интегрирования.
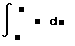
- Щёлкните на поле внизу и наберите 0. Щёлкните на
верхнем поле и нажмите клавиши p/4.
Так задаются верхний и нижний пределы
интегрирования.
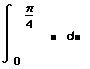
- Щёлкните на поле между знаком интеграла и d.
Затем напечатайте sin(x)^2. Это — выражение, которое
нужно интегрировать.
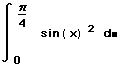
- Щёлкните на поле и наберите x. Это — переменная
интегрирования. Затем нажмите знак =, чтобы
увидеть результат.
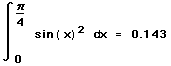
Для приближенного вычисления определенного
интеграла Mathcad использует численный алгоритм
интегрирования Ромберга.
Необходимо сделать следующие замечания
относительно численного интегрирования в Mathcad:
- Пределы интегрирования должны быть
вещественными. Выражение, которое нужно
интегрировать, может быть, однако, вещественным
либо комплексным.
- Кроме переменной интегрирования, все
переменные в подинтегральном выражении должны
быть определены ранее в другом месте рабочего
документа.
- Переменная интегрирования должна быть простой
переменной без индекса.
- Если переменная интегрирования
является размерной величиной, верхний и
нижний пределы интегрирования должны иметь ту же
самую размерность.
Подобно всем численным методам, точность
алгоритма интегрирования в Mathcad зависит от
особенностей подинтегрального выражения.
Если выражение, которое нужно интегрировать,
имеет особенности, разрывы или быстро
осциллирует, численное решение, найденное Mathcad,
может быть неточно.
Поскольку метод интегрирования Mathcad делит
интервал на четыре подинтервала, а затем
удваивает число точек разбиения, это может
привести к неправильным результатам для
периодических функций с периодом 1/2n от
длины интервала. Чтобы обойти эту проблему,
делите интервал на два подинтервала, не кратных
периоду функции, и интегрируйте по каждому
подинтервалу отдельно.
Для вычисления точного значения интеграла или
для нахождения неопределенного интеграла могут
быть использованы возможности символьных
вычислений Mathcad. Подробности см. в Главе “Символьные
вычисления”.
Переменные пределы интегрирования
Хотя результат интегрирования — одно число,
всегда можно использовать интеграл совместно с
дискретным аргументом, чтобы получить
результаты для многих значений параметра.
Например, можно задать переменный предел
интегрирования. На Рисунке 7 показано, как это
сделать.
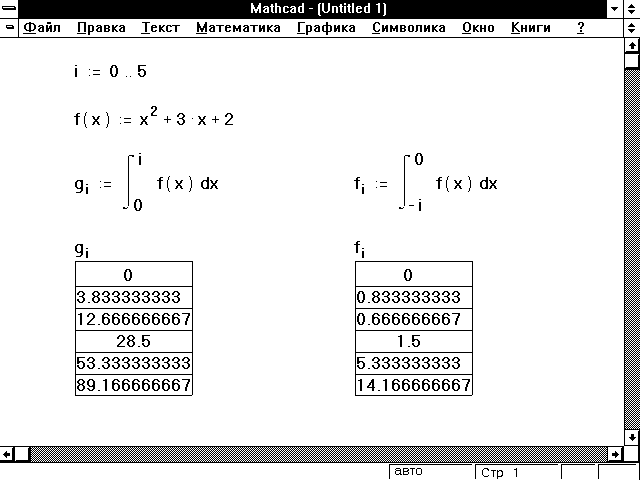
Рисунок 7: Переменные пределы интегрирования.
Отметим, что вычисления, подобные показанным на
Рисунке 7, могут потребовать неоднократного
вычисления интеграла. Это может привести к
значительным затратам машинного времени, в
зависимости от сложности интегралов, длины
интервала интегрирования и значения встроенной
переменной TOL.
Изменение точности вычисления интегралов
Численный алгоритм интегрирования Mathcad делает
последовательные вычисления значения интеграла,
увеличивая точность на каждом шаге, и возвращает
значение, когда два последних значения
отличаются меньше, чем на величину встроенной
переменной TOL. На Рисунке 8 показано, как
изменение значения TOL влияет на точность
вычисления интеграла. Чтобы вывести большее
количество значащих цифр.

Рисунок 8: Влияние значения встроенной
переменной TOL на вычисление интеграла.
При необходимости можно изменять точность
вычислений, включив определения для
значения TOL непосредственно в рабочий
документ, как показано на Рисунке 8. Можно также
сделать это с помощью команды Встроенные
переменные из меню Математика. Чтобы
увидеть эффект изменения точности вычислений,
выберите команду Пересчитать все из меню Математика
для повторного вычисления всех выражений в
рабочем документе. Если численный алгоритм Mathcad
не достигает заданной точности, Mathcad отмечает
интеграл сообщением об ошибке “не сходится”.
Эта ошибка может быть вызвана либо функцией,
которая имеет особенности, либо наличием
осцилляций в интервале интегрирования, либо
слишком длинным интервалом интегрирования. При
изменении точности необходимо помнить о
соблюдении компромисса между точностью и
временем вычисления, поскольку увеличение
точности требует увеличения времени вычислений.
Криволинейные и двойные интегралы
Mathcad может быть использован для вычисления
криволинейных интегралов в комплексной
плоскости. Для этого сначала параметризуйте
контур. Затем интегрируйте по параметру. Если
параметр отличен от длины дуги, необходимо также
включить производную параметризации как
поправочный коэффициент. Пример приведен на
Рисунке 9. Обратите внимание, что мнимая единица
i, которая использована в определении пути,
должна набираться как 1i.
В Mathcad можно также вычислять двойные или
кратные интегралоы. Чтобы ввести знак двойного
интеграла, наберите & дважды. Введите
подинтегральное выражение, пределы и переменные
интегрирования для каждого интеграла. На Рисунке
10 приведен пример.

Рисунок 9: Как в Mathcad вычислить криволинейный
интеграл по пути в комплексной плоскости.
Имейте в виду, что двойные интегралы
вычисляются дольше, чем простые интегралы. Везде,
где возможно, используйте эквивалентный простой
интеграл вместо двойного интеграла.

Рисунок 10: Двойные интегралы.
  
|

