  Оператор производной Mathcad
предназначен для нахождения численного значения
производной функции в заданной точке. Например,
чтобы найти производную x3 по x в точке x =
2, выполните следующее: Оператор производной Mathcad
предназначен для нахождения численного значения
производной функции в заданной точке. Например,
чтобы найти производную x3 по x в точке x =
2, выполните следующее:
- Сначала определите точку, в которой необходимо
найти производную. Наберите x:2.
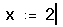
- Щёлкните ниже определения x. Затем наберите ? .Появляется
оператор производной с двумя полями,
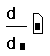
- Щёлкните на поле в знаменателе и наберите x. Это
имя переменной по которой проводится
дифференцирование.
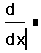
- Щёлкните на поле справа от d/dx и наберите x^3. Это
— выражение, которое нужно дифференцировать.
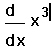
- Нажмите знак =, чтобы увидеть результат.
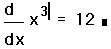

Рисунок 4: Примеры дифференцирования при помощи
Mathcad.
На Рисунке 4 показаны примеры
дифференцирования в Mathcad.
От алгоритма вычисления производной, который
используется в Mathcad, можно ожидать, что первая
производная будет вычислена с точностью 7 или 8
значащих цифр, если точка, в которой ищется
производная, удалена от особенностей функции.
Точность этого алгоритма уменьшается на одну
значащую цифру при каждом увеличении порядка
производной.
Необходимо помнить, что результат
дифференцирования есть не функция, а число —
значение производной в указанной точке
переменной дифференцирования. В предыдущем
примере производная от x3 не есть выражение
3x2, а значение 3x2, вычисленное в точке x
= 2. Информацию по поводу символьного вычисления
производных см. в Главе “Символьные
вычисления”.
Хотя дифференцирование возвращает только одно
число, можно определить одну функцию как
производную другой функции. Например:
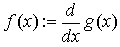
Вычисление f(x) будет возвращать в
численной форме производную g(x) в точке x.
Эта методика может быть использована для
вычисления производной функции в
последовательности точек. См. пример на Рисунке 5.

Рисунок 5: Вычисление производной функции в
последовательности точек.

Рисунок 6: Результаты вычисления производной
функции в различных точках, сохраненные как
элементы вектора.
Сделаем несколько замечаний относительно
численного дифференцирования в Mathcad:
- Выражение, которое нужно дифференцировать,
может быть вещественным или комплексным.
- Переменная дифференцирования должна быть
простой неиндексированной переменной. Для
вычисления производной в отдельных различных
точках — элементах вектора — используйте
методику, приведенную на Рисунке 6.
Производные более высокого порядка
В Mathcad существует оператор для вычисления
производной n-ного порядка.
Например, чтобы найти третью производную
функции x9 по x в точке x = 2, выполните
следующее:
- Сначала определите точку, в которой необходимо
вычислить производную. Наберите x:2.
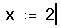
- Щёлкните ниже определения x. Затем нажмите
клавиши [Ctrl]? . Появляется оператор
производной с двумя полями в знаменателе,
одним в числителе и еще одним справа.
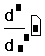
- Щёлкните на поле внизу и наберите x. Это имя
переменной, по которой производится
дифференцирование.
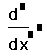
- Щёлкните на поле выше и правее от предыдущего
поля и наберите 3. Это должно быть целое число
между 0 и 5. Обратите внимание, что поле в
числителе автоматически отображает любой
порядок, печатаемый в знаменателе.
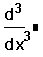
- Щёлкните на поле справа от d/dx и наберите x^9. Это
— выражение, которое нужно дифференцировать.
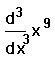
- Нажмите знак =, чтобы видеть третью
производную выражения в заданной точке.
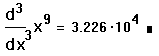
При n = 1 оператор дает тот же самый результат,
что и оператор производной, обсужденный выше. При
n = 0 он возвращает значение функции.
  
|

