Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример 4

Пример 1. Фазовые кривые автономной системы

Рассмотрим автономную систему дифференциальных уравнений

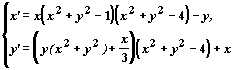
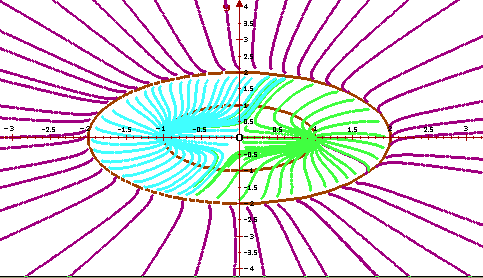
это нелинейная система второго порядка.Ниже приведен рисунок, выполненный программой ОДУ, на котором изображены фазовые кривые этой автономной системы.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Вернуться на страницу <Курс ОДУ. Примеры>

Пример 2. Типы фазовых кривых автономной системы

Рассмотрим автономную систему дифференциальных уравнений

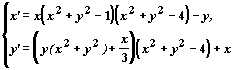
это нелинейная система второго порядка. Ниже приведен рисунок, выполненный программой ОДУ, на котором изображены фазовые кривые этой автономной системы. Видно, что фазовые кривые не пресекаются. Кажется, что есть "пучки", проходящие через точки (-1, 0) и (1, 0), но на самом деле эти гладкие кривые - фазовые, отвечающие решениям (x(t), y(t)), которые при t стремящемся к бесконечности стремятся к (-1, 0) и (1, 0). Система имеет также фазовые кривые - точки, отвечающие решениям x(t)=-1, y(t)=0 и x(t)=1, y(t)=0, и фазовые кривые - окружности, отвечающие решениям периодическим решениям x(t)=cos(t), y(t)=sin(t) и x(t)=2cos(t), y(t)=2sin(t).

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Вернуться на страницу <Курс ОДУ. Примеры>

Пример 3. Точки покоя автономной системы

Рассмотрим автономную систему дифференциальных уравнений

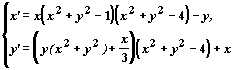
это нелинейная система второго порядка. Ниже приведен рисунок, выполненный программой ОДУ, на котором изображены фазовые кривые этой автономной системы.
На рисунке видно, что есть два семейства решений (x(t), y(t)), которые при t стремящемся к бесконечности стремятся к (-1, 0) и (1, 0). Легко убедиться подстановкой, что точки (-1, 0) и (1, 0) - это фазовые кривые, отвечающие решениям x(t)=-1, y(t)=0 и x(t)=1, y(t)=0. Подстановкой в правые части уравнений системы легко убедиться, что эти точки - точки покоя системы (в точках (-1, 0) и (1, 0) обе правые части уравнений системы обращаются в нуль).

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Вернуться на страницу <Курс ОДУ. Примеры>

Пример 4. Векторное поле автономной системы

Рассмотрим автономную систему дифференциальных уравнений

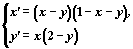
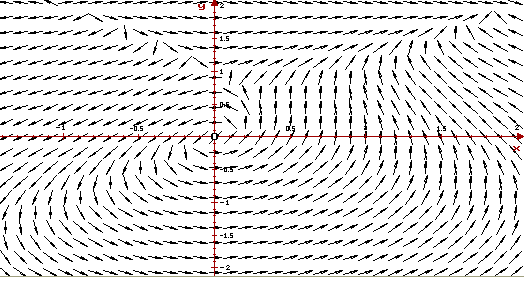
это нелинейная система второго порядка. Ниже приведен рисунок, выполненный программой ОДУ, на котором изображено векторное поле системы. Видно, что векторное поле - это фактически фазовый портрет системы, поскольку стрелки векторного поля дают полное представление о поведении соответствующих  фазовых кривых.

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Вернуться на страницу <Курс ОДУ. Примеры>