Пример 1 ~ Пример 2 ~ Пример 3
Пример 1. Приближение функции по методу наименьших
квадратов.
Пусть функция задана таблицей своих значений:
| x |
-3 |
-1 |
0 |
1 |
3 |
| y |
-4 |
-0.8 |
1.6 |
2.3 |
1.5 |
Приблизим функцию многочленом 2-ой степени. Для
этого вычислим коэффициенты нормальной системы
уравнений:
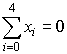 , , 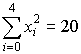 , , 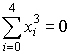 , , 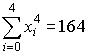
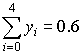 , , 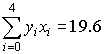 , , 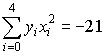
Составим нормальную систему наименьших
квадратов, которая имеет вид:
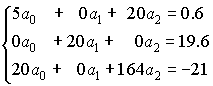
Решение системы легко находится: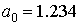 , , 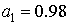 , , 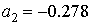 . .
Таким образом, многочлен 2-ой степени найден: 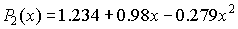 . .
Теоретическая справка

Пример 2. Нахождение оптимальной степени многочлена.

Пример 3. Вывод нормальной системы уравнений для
нахождения параметров эмпирической зависимости.
Выведем систему уравнений для определения
коэффициентов 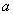 и и 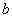 функции функции 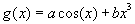 ,
осуществляющей среднеквадратичную
аппроксимацию заданной функции ,
осуществляющей среднеквадратичную
аппроксимацию заданной функции 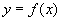 по по 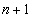 точкам.
Составим функцию точкам.
Составим функцию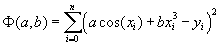 и запишем
для нее необходимое условие экстремума: и запишем
для нее необходимое условие экстремума:
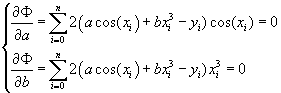
Тогда нормальная система примет вид:
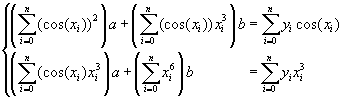
Получили линейную систему уравнений
относительно неизвестных параметров и, которая
легко решается.
Теоретическая справка

|

