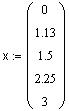
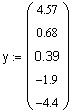
возвращает вектор a коэффициентов многочлена:
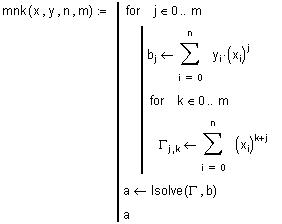
решает систему линейных алгебраических уравнений Ga=b
x, y - векторы исходных данных;
n+1 - размерность x,y.
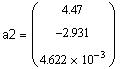
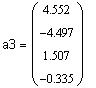
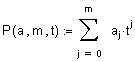
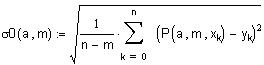
Графики многочленов степени 0,1,2,3 и точечный график исходной функции:
![]()
| Пример 2. Нахождение оптимальной степени многочлена | |||||
| Векторы исходных данных: | |||||
|
|
||||
| Функция mnk, строящая многочлен степени m по
методу наименьших квадратов, возвращает вектор a коэффициентов многочлена: |
|||||
|
- формирование вектора правой части и
матрицы нормальной системы Гa=b метода наименьших
квадратов (базисные функции - 1, x, , |
||||
| - встроенная функция MATHCAD, решает систему линейных алгебраических уравнений Ga=b |
|||||
| Входные параметры: x, y - векторы исходных данных; n+1 - размерность x,y. |
|||||
| Вычисление коэффициентов многочленов степени 0,1,2,3 по методу наименьших квадратов: | |||||
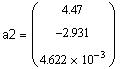 |
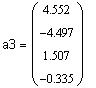 |
||||
| Функция P возвращает значение многочлена степени m в точке t;многочлен задается с помощью вектора коэффициентов a: |
|
||||
| Функция |
|||||
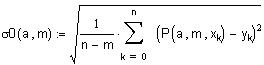 |
|||||
| Вычисление значений |
|||||
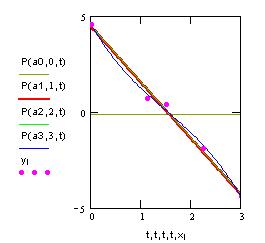
| Вывод : оптимальная степень m*=1;
многочлен наилучшего среднеквадратичного
приближения: P1(x)=4.465-2.917x Графики многочленов степени 0,1,2,3 и точечный график исходной функции: |
|||||
|
|||||
 |
|||||