Пример 1 ~ Пример 2 ~ Пример 3 ~ Пример
4
Пример 1. Решение системы методом Гаусса с выбором
главного элемента по столбцу.
Пусть Ax=b, где
A= 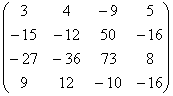 , b= , b= 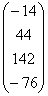
Прямой ход. 1 шаг . Максимальный по модулю
элемент 1-го столбца 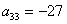 .
Переставим 1-ое и 3 - е уравнения местами: .
Переставим 1-ое и 3 - е уравнения местами:
A= 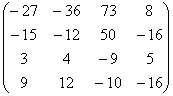 , b= , b= 
Вычислим масштабирующие множители 1 шага:
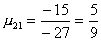 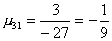 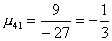
и выполним преобразование матрицы и вектора:
A1= 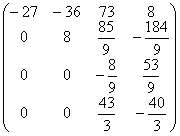 b1= b1= 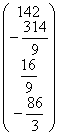
2 шаг. Вычислим масштабирующие множители 2 шага:
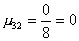 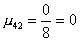 . .
Второй шаг не изменяет матриц: A2=A1, b2= b1.
3 шаг. Максимальный по модулю элемент 3 столбца 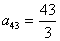 . Переставим 3 и 4 уравнения
местами. . Переставим 3 и 4 уравнения
местами.
A2= 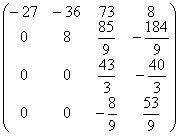 b2= b2= 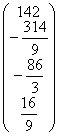
Вычислим масштабирующие множители 3 шага:
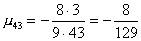
и выполним преобразование матрицы и вектора:
A3= 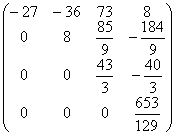 b3= b3= 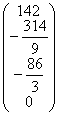
Обратный ход. Из последнего уравнения
находим: 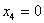 . Из третьего . Из третьего
уравнения системы находим 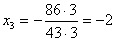 . Из второго уравнения находим . Из второго уравнения находим
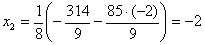 . Неизвестное . Неизвестное 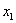 находим из первого уравнения: находим из первого уравнения:
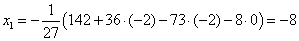
Ответ: 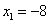 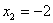 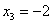 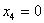 . .

Пример 2. Решение системы методом Холецкого.
Пусть
A= 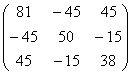 b= b= 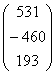
Находим элементы матрицы L:
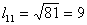 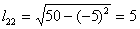 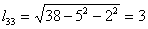
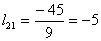 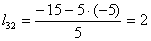
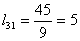
Таким образом разложение матрицы A имеет
вид:
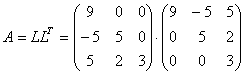
Последовательно решаем системы 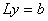 и и 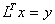 .
Решением 1-ой системы является вектор .
Решением 1-ой системы является вектор 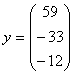 , а решение 2-ой системы вектор , а решение 2-ой системы вектор 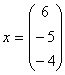 . .
Ответ: 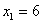 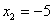 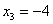

Пример 3. Разложение матриц на множители.

Пример 4.
Решение системы уравнений методом прогонки.
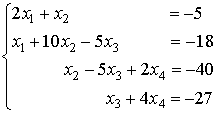
Прямой ход прогонки. Вычислим прогоночные
коэффициенты:
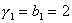 , , 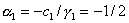 , , 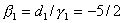
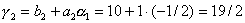 , , 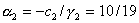 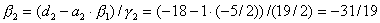
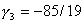 , , 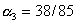 , , 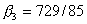
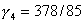 , , 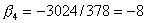
Обратный ход прогонки. Находим значения
неизвестных:
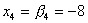 , , 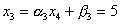 , , 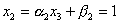 , , 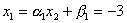
Ответ: 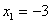 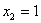 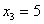 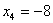 . .
Теоретическая справка

|

