Постановка задачи
приближенного решения уравнений ~ Этапы
решения задачи ~ Метод бисекций ~ Метод Ньютона ~ Метод простой
итерации
Метод решения задачи называют прямым,
если он позволяет получить решение после
выполнения конечного числа элементарных
операций. Метод решения задачи называют итерационным,
если в результате получают бесконечную
последовательность приближений к решению. Если
эта последовательность сходится к решению
задачи, то говорят, что итерационный процесс
сходится. К прямым методам решения относятся
метод Гаусса и его модификации, метод Холецкого и
метод прогонки.
В методе Гаусса для вычисления
масштабирующих множителей требуется делить на
ведущие элементы каждого шага. Если элемент
равен нулю или близок к нулю, то возможен
неконтролируемый рост погрешности.
Поэтому часто применяют модификации метода
Гаусса, обладающие лучшими вычислительными
свойствами.
Метод Гаусса с выбором главного элемента по
столбцу (схема частичного выбора). На k-ом
шаге прямого хода в качестве ведущего элемента
выбирают максимальный по модулю коэффициент 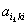 при
неизвестной при
неизвестной 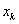 в уравнениях с номерами i = k+1, ... , m.Затем
уравнение, соответствующее выбранному
коэффициенту с номером в уравнениях с номерами i = k+1, ... , m.Затем
уравнение, соответствующее выбранному
коэффициенту с номером 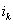 , меняют местами с к-ым
уравнением системы для того, чтобы главный
элемент занял место коэффициента , меняют местами с к-ым
уравнением системы для того, чтобы главный
элемент занял место коэффициента 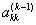 . После
этой перестановки исключение проводят как в
схеме единственного деления. В этом случае все
масштабирующие множители по модулю меньше
единицы и схема обладает вычислительной
устойчивостью. . После
этой перестановки исключение проводят как в
схеме единственного деления. В этом случае все
масштабирующие множители по модулю меньше
единицы и схема обладает вычислительной
устойчивостью.

ПРИМЕР 1.Решение системы
методом Гаусса с выбором главного элемента по
столбцу.
Метод Холецкого. Если матрица
системы является симметричной и положительно
определенной, то для решения системы применяют
метод Холецкого (метод квадратных корней). В
основе метода лежит алгоритм специального LU-разложения
матрицы A, в результате чего она приводится к
виду A=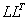 .
Если разложение получено, то как и в методе LU-разложения,
решение системы сводится к последовательному
решению двух систем с треугольными матрицами: .
Если разложение получено, то как и в методе LU-разложения,
решение системы сводится к последовательному
решению двух систем с треугольными матрицами: 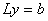 и и 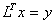 . Для
нахождения коэффициентов матрицы L неизвестные
коэффициенты матрицы . Для
нахождения коэффициентов матрицы L неизвестные
коэффициенты матрицы 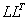 приравнивают
соответствующим элементам матрицы A. Затем
последовательно находят требуемые коэффициенты
по формулам: приравнивают
соответствующим элементам матрицы A. Затем
последовательно находят требуемые коэффициенты
по формулам:
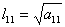 , , 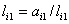 i = 2, 3, ...,
m, i = 2, 3, ...,
m,
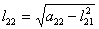 , , 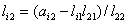 i = 3, 4, ...,
m, i = 3, 4, ...,
m,
...............
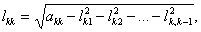 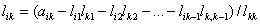 i
= k+1, ... , m. i
= k+1, ... , m.
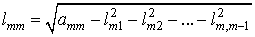

ПРИМЕР 2. Решение системы
методом Холецкого.

ПРИМЕР 3. Разложение матриц
на множители.
Метод прогонки.Если матрица
системы является разреженной, то есть содержит
большое число нулевых элементов, то применяют
еще одну модификацию метода Гаусса - метод
прогонки. Рассмотрим систему уравнений с
трехдиагональной матрицей:
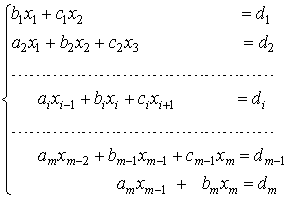
Преобразуем первое уравнение системы к виду 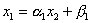 , где , где 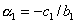 , , 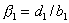
Подставим полученное выражение во второе
уравнение системы и преобразуем его к виду 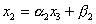 и т.д. На
i-ом шаге уравнение преобразуется к виду и т.д. На
i-ом шаге уравнение преобразуется к виду 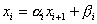 , где , где 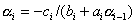 , , 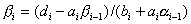 . На m-ом
шаге подстановка в последнее уравнение
выражения . На m-ом
шаге подстановка в последнее уравнение
выражения 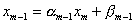 дает возможность определить значение дает возможность определить значение 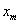 : :
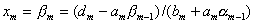 .
Значения остальных неизвестных находятся по
формулам: .
Значения остальных неизвестных находятся по
формулам: 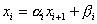 , i = m-1, m-2, ..., 1. , i = m-1, m-2, ..., 1.
ПРИМЕР 4. Решение системы
методом прогонки.

|

