Функция-оригинал
~ Преобразование Лапласа ~ Основные
свойства преобразования Лапласа ~ Алгоритм
решения Задачи Коши для уравнений ~ Алгоритм
решения Задачи Коши для систем
Операционное исчисление - один из
наиболее эффективных методов интегрирования
линейных дифференциальных уравнений с
постоянными коэффициентами. При решении
операционным методом задача интегрирования
линейного дифференциального уравнения с
постоянными коэффициентами сводится к задаче о
решении алгебраического уравнения.
Функцией-оригиналом называется
функция f (x) для которой
справедливо:
f (x) непрерывна при неотрицательных x,
за исключением, быть может конечного числа точек,
f (x) = 0 при x<0, существуют такие
постоянные M и a, что 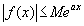 при всех
неотрицательных x. при всех
неотрицательных x.
Преобразованием Лапласа функции f (x)
называется функция 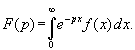
Функция F (p) называется
изображением функции f (x), а функция f (x)
- оригиналом для F (p).
ПРИМЕР 1. Отыскание изображения и оригинала.
Основные свойства
преобразования Лапласа, используемые при
решении дифференциальных уравнений следующие:
- оригинал восстанавливется по изображению
единственным образом, с точностью до значений в
точках разрыва - теорема единственности;
- если F (p) и G (p) -
изображения соответственно для f (x) и
g (x), то изображением для af (x) + bg (x)
является aF (p) + bG (p) -
линейность преобразования Лапласа;
- изображением для производной f (n)(x)
является функция pnF(p) - pn-1f (0) - pn-2f '(0) -...-
pf (n-2)(0) - f (n-1)(0) - изображение
производных;
- если F (p) изображения для f (x),
то для любого a>0 изображением для f (x-a)
является
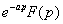 - теорема запаздывания. - теорема запаздывания.
Рассмотри задачу Коши:
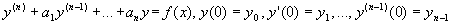
a1, a2, ..., an
- постоянные.
Алгоритм решения задачи Коши для
уравнений операционным методом состоит в
следующем. Обрзначим Y (p) и F (p)
изображения для y (x) и f (x).
Тогда по основным свойствам преобразования
Лапласа, переходя к изображениям, получим: 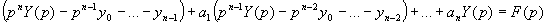
или, A (p)Y (p) + B (p)
= F (p), где A (p) и B (p)
- многочлены.
Отсюда:
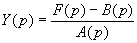
и искомое решение задачи Коши y (x)
является оригиналом для Y (p).
ПРИМЕР 2. Решение задачи Коши для линейного
дифференциального уравнения с постоянными
коэффициентами.
Совершенно аналогично операционное исчисление
применяется к решению задачи Коши для систем
линейных дифференциальных уравнений с
постоянными коэффициентами. Рассмотри задачу
Коши:
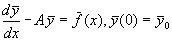
A- постоянна матрица размерности n.n.
Алгоритм решения задачи Коши для систем
операционным методом состоит в следующем.
Обозначим 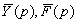 изображения для изображения для 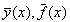 -
компонентами вектор-функций -
компонентами вектор-функций 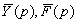 являются
изображения соответствующих компонент
вектор-функций являются
изображения соответствующих компонент
вектор-функций 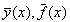 . Тогда по основным свойствам
преобразования Лапласа, переходя к изображениям,
получим: . Тогда по основным свойствам
преобразования Лапласа, переходя к изображениям,
получим:
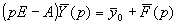
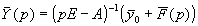 , ,
где E - единичная матрица, 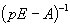 - обратная
матрица к матрице - обратная
матрица к матрице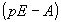 . Тогда искомое решение
задачи Коши . Тогда искомое решение
задачи Коши 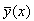 является оригиналом для является оригиналом для 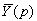 . .
ПРИМЕР 3. Решение задачи Коши для системы
линейных дифференциальных уравнений с
постоянными коэффициентами.

|

