Пример 1 ~ Пример 2 ~ Пример 3

Пример 1. Вычислить интеграл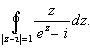  

Решение. Особыми точками подынтегральной функции являются нули знаменателя - корни уравнения exp(z) - i = 0, т.е. точки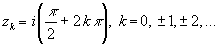  

Кругу 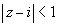принадлежит только одна из этих точек, точка  

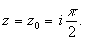
Эта точка - простой полюс функции 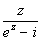  , т.к. она является простым нулем знаменателя.

Вычислим вычет в простом полюсе f (z):

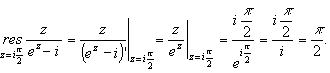
Тогда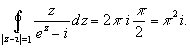

Решение примера в среде пакета Mathcad		Теоретическая справка
Решение примера в среде пакета Mathematica

Пример 2. Вычислить интеграл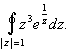  

Решение. Единственная особая точка подынтегральной функции - существенно особая точка z = 0. Она принадлежит области, ограниченной контуром интегрирования.

Вычислим вычет в существенно особой точке функции f (z): 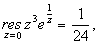  поскольку

Тогда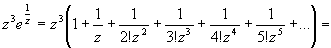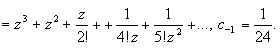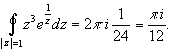

Решение примера в среде пакета Mathematica

Теоретическая справка

Пример 3. Вычислить интеграл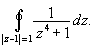  

Решение. Особыми точками подынтегральной функции являются нули знаменателя - корни уравнения z⁴ + 1 = 0, т.е. точки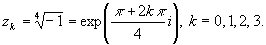  

Все эти точки - простые полюсы подынтегральной функции, кругу 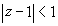     принадлежат только две из них: 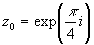     и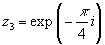  

Вычислим вычеты f(z) в этих точках:

Тогда

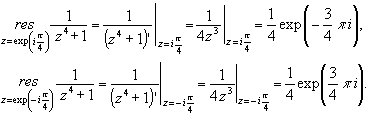
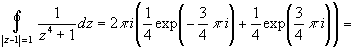
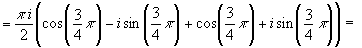
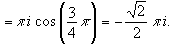
Решение примера в среде пакета Mathematica

Теоретическая справка