Пример 1
~ Пример 2 ~ Пример 3
~ Пример 4 ~ Пример 5
~ Пример 6
Пример 1. Фундаментальная
система решений и общее решение для случая
простых действительных корней
Рассмотрим уравнение y'' - 3y' + 2y
= 0.
Его характеристическое уравнение l2 - 3l + 2 = 0
имеет два различных действительных корня l1 =1 и l2 =2.
Фундаментальная система решений уравнения:
y1 = exp(l1x)=exp(x)
и y2 = exp(l2x)=exp(2x)
Общее решение уравнения: y(x) = c1exp(x)
+ c2exp(2x).

Пример 2. Фундаментальная
система решений и общее решение для случая
кратных действительных корней
Рассмотрим уравнение y''- 2y' + y = 0.
Его характеристическое уравнение l2 - 2l + 1 = 0
имеет один кратный действительный корень l1 = l2 = 1.
Фундаментальная система решений уравнения: y1
= exp(x) и y2= xexp(x)
Общее решение уравнения: y(x) = c1exp(x)
+ c2xexp(x).

Пример 3. Фундаментальная
система решений и общее решение для случая
простых комплексных корней
Рассмотрим уравнение y'' - 2y' + 5y = 0.
Его характеристическое уравнение l2 - 2l + 5 = 0
имеет пару комплексно сопряженных корней l1 = 1-2i, l2
= 1+ 2i.
Фундаментальная система решений уравнения: exp(x)cos2x,
exp(x)sin2x.
Общее решение уравнения: y(x) = c1exp(x)cos2x
+ c2exp(x)sin2x.

Пример 4. Фундаментальная
система решений и общее решение для случая
простых комплексных корней. Мнимые корни
Рассмотрим уравнение y'' + y = 0.
Его характеристическое уравнение l2 + 1 = 0
имеет пару комплексно сопряженных корней l1 =i, l2 =
-i.
Фундаментальная система решений уравнения: cosx,
sinx
Общее решение уравнения: y(x) = c1cosx
+ c2sinx.

Пример 5. Фундаментальная
система решений и общее решение для случая
кратных комплексных корней
Рассмотрим уравнение y''''- 4y''' + 14y''
- 20y' + 25y = 0.
Его характеристическое уравнение l4-
4l3 + 14l2
- 20l + 25 = 0
имеет пару кратных комплексно сопряженных
корней
l1,2 =1- 2i, l3,4
= 1 + 2 i.
Фундаментальная система решений уравнения:
y1 = exp(x)cos2x, y2= exp(x)sin2x,
y3 = xexp(x)cos2x и y4
= xexp(x)sin2x.
Общее решение уравнения:
y(x) = c1exp(x)cos2x + c2exp(x)sin2x
+ c3xexp(x)cos2x + c4xexp(x)sin2x.

Пример 6. Решение задачи Коши
Рассмотрим задачу Коши для однородного
дифференциального уравнения
y'' + 2y' + 3y = 0, y(0) = 1, y'(0) = 1.
Его характеристическое уравнение l2 + 2l + 3 = 0
имеет пару комплексно сопряженных корней l1 = -1-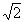 i, l2 = -1 + i, l2 = -1 + 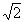 i. i.
Фундаментальная система решений содержит два
решения
exp(-x)cos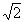 x,
y=exp(-x)sin x,
y=exp(-x)sin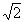 x, x,
его общее решение имеет вид
y(x) = c1exp(-x)cos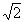 x + c2exp(-x)sin x + c2exp(-x)sin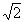 x. x.
Решение задачи Коши y(0)=1, y'(0)=1 находим из
условий
y(0) = c1exp(0)cos(0) + c1exp(0)sin(0) = c1
=1,
y'(0) = -c1exp(0)cos(0) -c1 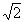 exp(0)sin(0) - c2exp(0)sin(0)
+ c2 exp(0)sin(0) - c2exp(0)sin(0)
+ c2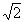 exp(0)cos(0)
= exp(0)cos(0)
=
= - c1 + 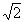 c2 =1, откуда c1 = 1 и c2
=
c2 =1, откуда c1 = 1 и c2
= 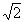 . Подставив
константы в выражение для общего решения получим
решение задачи Коши . Подставив
константы в выражение для общего решения получим
решение задачи Коши
y(x) = exp(-x)cos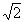 x + x + 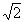 exp(-x)sin exp(-x)sin
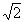 x. x.

|

