Определение численного решения ~ Одношаговый численный метод ~ Метод Эйлера Геометрическая интерпретация метода Эйлера ~ Метод Рунге-Кутты 4 порядка ~ Правило Рунге оценки погрешности

Если задачу об отыскании всех решений дифференциального уравнения удается свести к конечному числу алгебраических операций, операций интегрирования и дифференцирования известных функций, то говорят, что уравнение интегрируется в квадратурах. В приложениях крайне редко встречаются уравнения, интегрируемые в квадратурах. Поэтому для исследования дифференциальных уравнений широко используются приближенные, численные методы их решения.

Численное решение на отрезке [a, b] задачи Коши
y' = f(x, y),  y(a) = y₀
состоит в построении таблицы приближенных значений
y₀, y₁, ..., y_i, ... y_N
решения y(x) в узлах сетки
a=x₀ < x₁ < ... < x_i < ...< x_N=b,  y(x_i)@ y_i.
Если x_i = a+ i h, h=(b-a)/ N, то сетка 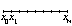    называется равномерной.

Численный метод решения задачи Коши называется одношаговым, если для вычисления решения в точке x₀ + h используется информация о решении только в точке x₀.

Простейший одношаговый метод численного решения задачи Коши - метод Эйлера. В методе Эйлера величины y_i   вычисляются по формуле
y_i+1 = y_i + h f(x_i , y_i),   i = 0, 1, ...

ПРИМЕР 1. Решение задачи Коши методом Эйлера.

ПРИМЕР 2. Решение задачи Коши методом Эйлера с шагом h и h/2.

Метод Эйлера допускает простую геометрическую интерпретацию. Пусть известна точка (x_i, y_i) интегральной кривой уравнения y'=f(x, y).
Касательная к интегральной кривой уравнения, проходящая через эту точку, определяется уравнением
y = y_i + f(x_i , y_i)(x-x_i).
Следовательно, вычисленная методом Эйлера точка (x_i+1 , y_i+1 ),
где x_i+1=x_i+h, y_i+1=y_i + h f(x_i , y_i), лежит на этой касательной.

ПРИМЕР 3. Геометрическая интерпретация метода Эйлера.

Методом Рунге-Кутты четвертого порядка точности называют одношаговый метод, относящийся к широкому классу методов Рунге-Кутты. В этом методе величины y_i+1 вычисляются по следующим формулам:
y_i+1 = y_i + h (k₁ + 2k₂ + 2k₃ + k₄)/6 ,   i = 0, 1, ...
k₁ = f(x_i , y_i),
k₂ = f(x_i+h/2, y_i+hk₁/2),
k₃ = f(x_i+h/2, y_i+hk₂/2),
k₄ = f(x_i+h, y_i+hk₃).

ПРИМЕР 4. Решение задачи Коши методом Рунге-Кутты 4-го порядка.

ПРИМЕР 5. Сравнение приближенных решений, вычисленных методом Эйлера и Рунге-Кутты.

Практически оценить погрешность численного метода позволяет правило Рунге. Сначала вычисляют приближенное решение с шагом h, затем -  с шагом h/2. Тогда для метода Рунге-Кутты 4 порядка точности справедливо приближенное равенство
y(x_2i) -  y_2i^(h/2) @ (y_2i^(h/2) - y_i^(h))/15,
здесь y_i^(h) - приближенное решение, вычисленное с шагом h,
y_2i^(h/2) - приближенное решение, вычисленное с шагом h/2.
За оценку погрешности решения, вычисленного с шагом h/2, принимают величину
max_i|y_2i^(h/2) - y_i^(h) |/15.

ПРИМЕР 6. Решение задачи Коши методом Рунге-Кутты с шагом h и h/2, оценка погрешности.