Производные
высших порядков ~ Дифференциалы
высших порядков ~ Понятие
инвариантности формы дифференциала
Производные высших порядков.
Рассмотрим функцию 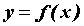 , определенную на
некотором промежутке , определенную на
некотором промежутке 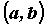 . Вычислим производную . Вычислим производную 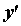 ,
которая также является функцией на ,
которая также является функцией на 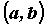 .
Производной второго порядка от функции .
Производной второго порядка от функции 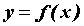 называется производная от ее производной:
называется производная от ее производной: 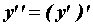 .
Аналогично определяют производную любого
порядка: .
Аналогично определяют производную любого
порядка: 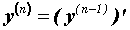 . .
ПРИМЕР 1 . Вычисление
производных высших порядков
Дифференциалы высших порядков.
Рассмотрим дифференциал
функции 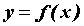 в произвольной точке промежутка в произвольной точке промежутка 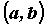 : : 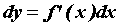 . Здесь . Здесь 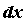 - приращение независимой
переменной, которое является числом и не зависит
от - приращение независимой
переменной, которое является числом и не зависит
от 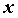 .
Сам же дифференциал есть функция от .
Сам же дифференциал есть функция от 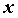 , и можно
вычислить дифференциал от этой функции: , и можно
вычислить дифференциал от этой функции: 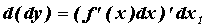 При При 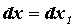 этот
дифференциал от дифференциала называется
дифференциалом второго порядка и вычисляется по
формуле этот
дифференциал от дифференциала называется
дифференциалом второго порядка и вычисляется по
формуле 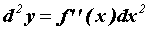 Аналогично вычисляется дифференциал
любого порядка Аналогично вычисляется дифференциал
любого порядка 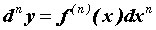 . .
ПРИМЕР 2 . Вычисление
дифференциалов высших порядков
Понятие инвариантности формы
дифференциала.
Рассмотрим дифференциал функции 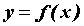 в
произвольной точке промежутка в
произвольной точке промежутка 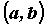 : : 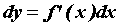 . Здесь . Здесь 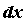 -
приращение независимой переменной, которое
является числом и не зависит от -
приращение независимой переменной, которое
является числом и не зависит от 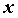 . Пусть теперь . Пусть теперь 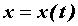 -
функция независимого переменного -
функция независимого переменного 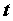 ,
определенная на промежутке ,
определенная на промежутке 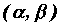 . Тогда . Тогда 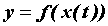 -
сложная функция переменного -
сложная функция переменного 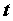 . Вычислим ее
дифференциал, используя формулу для производной сложной
функции: . Вычислим ее
дифференциал, используя формулу для производной сложной
функции: 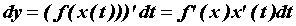 . Заметим, что . Заметим, что 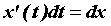 и выражение для
дифференциала принимает ту же форму и выражение для
дифференциала принимает ту же форму 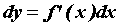 , хотя
здесь , хотя
здесь 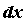 уже функция переменного
уже функция переменного 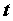 . Это свойство
дифференциала первого порядка называется
инвариантностью (т.е. неизменностью) его формы.
При вычислении дифференциала второго порядка
придется учитывать, что . Это свойство
дифференциала первого порядка называется
инвариантностью (т.е. неизменностью) его формы.
При вычислении дифференциала второго порядка
придется учитывать, что 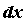 - функция
переменного - функция
переменного 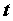 . Поэтому . Поэтому 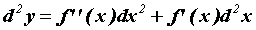 и форма второго (а
также и всех следующих) дифференциала
неинвариантна. и форма второго (а
также и всех следующих) дифференциала
неинвариантна.

|

