Производная
сложной функции ~ Производная
обратной функции
Производная сложной функции.
Пусть 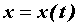 - функция, дифференцируемая
в точке - функция, дифференцируемая
в точке 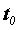 , , 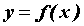 - функция, дифференцируемая в точке - функция, дифференцируемая в точке 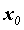 ,
причем ,
причем 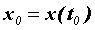 . Тогда . Тогда 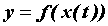 - сложная функция
независимого переменного - сложная функция
независимого переменного 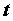 , дифференцируема в
точке , дифференцируема в
точке 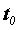 и ее производная
в этой точке вычисляется по формуле и ее производная
в этой точке вычисляется по формуле 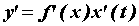 . .
Обычно 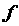 называют внешней функцией, а называют внешней функцией, а 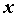 -
внутренней. При вычислении производной сложной
функции сначала дифференцируют внешнюю функцию,
не обращая внимания на внутреннюю (ведь она может
быть любой), затем умножают на производную
конкретной внутренней функции. -
внутренней. При вычислении производной сложной
функции сначала дифференцируют внешнюю функцию,
не обращая внимания на внутреннюю (ведь она может
быть любой), затем умножают на производную
конкретной внутренней функции.
ПРИМЕР 1 . Вычисление
производных сложных функций
Производная обратной функции.
Пусть функция 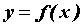 дифференцируема и
строго монотонна на дифференцируема и
строго монотонна на 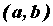 . Пусть также в точке . Пусть также в точке 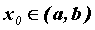 производная производная
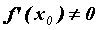 .
Тогда в точке .
Тогда в точке 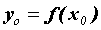 определена дифференцируемая
функция определена дифференцируемая
функция 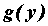 , которую называют обратной к , которую называют обратной к 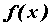 , а ее
производная вычисляется по формуле , а ее
производная вычисляется по формуле 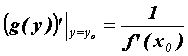 . .
ПРИМЕР 2 . Вычисление
производных обратной функции

|

