Пример 1
~ Пример 2 ~ Пример 3
~ Пример 4 ~ Пример 5
~ Пример 6
~ Пример 7
Пример 1. Найти вектор, выраженный через заданный
Для данного вектора а найти
вектор b, такой что а
 b, |b|=2∙|a|; b, |b|=2∙|a|;
вектор с, такой что а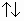 с, |с|=|a|/4; с, |с|=|a|/4;
вектор d, такой что a||d, |d|=3∙|a|;
вектор e, такой что a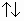 e, |e|=1. e, |e|=1.
Решение: по определению 11.
b=2∙a;
c=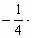 a; a;
вектор d находится неоднозначно: d1 a => d1=3∙a,
d2
a => d1=3∙a,
d2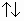 a => d2=-3∙
a; a => d2=-3∙
a;
e=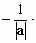 a. a.

Пример 2. Доказать свойство координат коллинеарных векторов
Доказать свойство 3 координат вектора.
Решение: Пусть b1={x1, y1, z1}
B, b2={x2, y2, z2}
B.
b1 || b2 ó
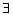 λ λ  R, т.ч. b1= λ∙b2.
R, т.ч. b1= λ∙b2.
<=> x1= λ∙x2, y1=
λ∙y2, z1= λ∙z2 <=>
λ=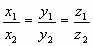 , если разрешить преобразовывать к нужному виду выражение
0= λ∙0. , если разрешить преобразовывать к нужному виду выражение
0= λ∙0.
Утверждение доказано.

Пример 3. Проверка коллинеарности векторов
Пусть в декартовой системе координат a={-1,5,2}, b={3,2,-2}.
Выяснить, будут ли коллинеарны векторы:
а) с и d, если с=а+b,
d=a-b;
b) е и f, если e= 2a+4b, f = -a-2b.

Пример 4. Найти координаты середины отрезка
Пусть в данной системе координат даны точки
A(1,2,3) и B(5,4,3). Найти координаты т.С, т.ч. АВ=2АС

Пример 5. Разложение вектора в заданном базисе
Пусть в декартовой системе координат a={1,0,1}, b={0,2,-1}, c={3,1,0},
d={-1,0,4}.
а) Выяснить, будет ли тройка a, b, c линейно независима.
б) разложить вектор d по базису B: a, b, c;
записать координаты d в этом базисе.

Пример 6. Вычислить координаты векторов
Вычислить координаты векторов b, c, d и e в условиях примера 1,
считая, что вектор a={x,y,z}.

Пример 7. Вычислить длины сторон треугольника
Пусть в декартовой системе координат точки А, В, и С имеют координаты:
A=(1,0,0), В=(0,5,-1), С=(-2,1,2).
a)Вычислить координаты векторов АВ, АС, СВ.
б) Найти длины сторон треугольника АВС.

|

