|
§ 2. Операции над свободными векторами:
сложение и умножение на число.
Определение 9: Сумма свободных векторов.
Пусть a, b  V3. Возьмем произвольно точку О. V3. Возьмем произвольно точку О.
Тогда 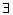 ! ОА ! ОА
 a и a и 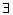 ! AB ! AB
 b т.ч. OB b т.ч. OB  a+b, т.е. a+b = { CD : CD = OB}
a+b, т.е. a+b = { CD : CD = OB}Корректность сложения: OB
 a+b, O'B' a+b, O'B'  a+b a+b  OB = O'B'. OB = O'B'.
Определение 10: Пусть a - свободный вектор, AB – его реализация, тогда BA является реализацией свободного вектора (-a).
(-a) – обратный вектор для a, т.е. (-a) = { BA : AB  a } a }
Определение 11: Умножение вектора на число:
1) λ•θ = θ для  λ λ  R. R.2) a ≠ θ, AB  a, отрезок AB лежит на прямой l. a, отрезок AB лежит на прямой l.
2.1) λ = 0 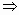 λ∙a = θ. λ∙a = θ.2.2) λ > 0 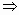 AC AC   λ∙a, где AC т.ч. |AC| = λ•|AB|, C λ∙a, где AC т.ч. |AC| = λ•|AB|, C  l и т. B и C находятся по одну сторону от т. А. l и т. B и C находятся по одну сторону от т. А.
2.3) λ < 0 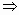 AD AD  λ∙a,
где AD т.ч. |AD| = |λ|∙|AB|, D λ∙a,
где AD т.ч. |AD| = |λ|∙|AB|, D  l и т. B и D находятся по разные стороны от
т. А. l и т. B и D находятся по разные стороны от
т. А.
Свойства операций над векторами:  a, b, c a, b, c  V3 , V3 ,  λ, μ λ, μ  R R
1) Коммутативность сложения
a + b = b + a.
2) Ассоциативность сложения
a + b + c = (a + b)+ c = a +( b + c).
3) a + θ = a.
4) a +(-a) = θ.
5) Ассоциативность умножения на число
λ(μ∙ a) = (λμ)∙ a
6) 1∙ a = a.
7) Дистрибутивность умножения на число относительно сложения векторов
λ∙( a + b) = λ∙ a +λ∙ b.
8) Дистрибутивность умножения на число относительно сложения чисел
(λ+μ)∙ a = λ∙ a +μ∙ a.
Пример 1
Найти вектор, выраженный через заданный


|

