|
§ 3. Линейная зависимость векторов. Коллинеарность и компланарность векторов.
Определение 12: Векторы а1, а2, … , аn
коллинеарны, если существует прямая l, содержащая реализацию каждого из них.
Обозначение: а || b
Предложение 2: a || b ó
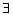 λ λ  R, т.ч. a= λ∙b R, т.ч. a= λ∙b
Определение 13: Коллинеарные векторы а и
b одинаково направлены,
если ОА а, ОВ а, ОВ b
и т. А и В лежат по одну сторону от т. О. b
и т. А и В лежат по одну сторону от т. О.
Обозначение: а  b b
Определение 14: Коллинеарные векторы а и
b разнонаправлены,
если ОА а, ОВ а, ОВ b
и т. А и В лежат по разные стороны от т. О. b
и т. А и В лежат по разные стороны от т. О.
Обозначение: а 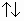 b b
Определение 15: Векторы а1, а2, … , аn
компланарны, если существует плоскость в пространстве, содержащая реализацию каждого из них.
Пример : рассмотрим с.в. еа=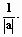 а ( а≠ θ ). а ( а≠ θ ).
еа коллинеарен а, одинаково направлен с а, |ea|=1.
Замечание: Любые два свободных вектора компланарны.
Нулевой вектор имеет реализацию на любой плоскости в пространстве.
Следовательно, три вектора: а, b, θ всегда компланарны.
Определение 16: Система векторов а1, а2, … ,
аn линейно зависима, если 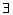 λ1,
λ2, …, λ3 λ1,
λ2, …, λ3 R,
не все равные нулю, такие что λ1· а1+ λ2·
а2+ λn· аn=0 R,
не все равные нулю, такие что λ1· а1+ λ2·
а2+ λn· аn=0
Определение 17: Если λ1· а1+ λ2·
а2+ λn· аn=0 только при λ1 = λ
2 = … = λ3 = 0, то система векторов а1, а2, … ,
аn линейно независима.
Предложение 3: Любая система из трёх и более ненулевых компланарных векторов
линейно зависима.
Предложение 4: Любые три некомпланарных вектора линейно независимы.


|

