|
§ 4. Проекции закреплённых и свободных векторов на плоскость и прямую.
Проецирование точек на плоскости и прямые хорошо изучается в школьном курсе геометрии,
так что остаётся уговориться об обозначениях:
прΠ М; – ортогональная проекция т. М на плоскость Π,
прm М; ( || l ) – проекция т. М на прямую m параллельно прямой
l
4.1 Ортогональная проекция на плоскость
Определение 18: Пусть А1= прΠ А,
В1= прΠ B 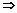 A1B1= прΠ
AB. A1B1= прΠ
AB.
( Т.е. з.в. A1B1 – это
ортогональная проекция з.в. AB на плоскость Π )
Определение 19: Пусть АВ
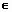 а и
прΠ AB а и
прΠ AB 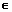 а1 а1 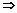 а1= прΠ а. а1= прΠ а.
( Т.е. с.в. а1 – это
ортогональная проекция с.в. а на плоскость Π )
4.2 Общий случай проецирования на плоскость.
( Проецирование параллельно прямой l которая не || и не лежит на плоскости Π )
Начало и конец вектора проецируются на Π параллельно l ,
определения вводятся аналогично п. 4.1 .
4.3 Ортогональная проекция на прямую
Определение 20: Пусть А1= прm А,
В1= прm B 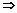 A1B1= прm
AB.] A1B1= прm
AB.]
Определение 21: Пусть АВ
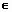 а и
прm AB а и
прm AB 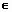 а1 а1
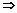 а1= прm а. а1= прm а.
4.4 Общий случай проецирования на прямую.
( Проецирование параллельно прямой l которая не || и не совпадает с прямой m )
Начало и конец вектора проецируются на m параллельно l ,
определения вводятся аналогично п. 4.3 .

|

