|
§ 5. Базисы в V3. Координаты векторов относительно базиса.
Определение 22: Базисом в пространстве свободных векторов V3
называется любая упорядоченная тройка некомпланарных векторов.
Пусть В : а1, а2, а3 – фиксированный базис в
V3.
Определение 23: Координатами вектора b относительно базиса В
называется упорядоченная тройка чисел {x, y, z}, т.ч. b=x·a1+
y·а2+z· а3.
Обозначение: b={x, y, z}B
Замечание: Под координатами закреплённого вектора понимают координаты соответствующего
ему свободного вектора.
Теорема1: Соответствие между V3 и R3 при фиксированном базисе
взаимно однозначно, т.е.  b b
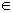 V3 V3 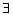 ! {x, y, z}
! {x, y, z}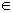 R3 и R3 и
 {x, y, z} {x, y, z}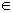 R3
R3 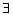 ! b ! b 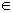 V3, т.ч. b={x, y, z}B
V3, т.ч. b={x, y, z}B
Соответствие между вектором и его координатами в данном базисе обладает следующими свойствами:
- Пусть b1={x1, y1, z1}B,
b2={x2, y2, z2}B
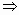 b1+ b2={x1+ x2, y1+ y2,
z1+ z2}B
b1+ b2={x1+ x2, y1+ y2,
z1+ z2}B
- Пусть b={x, y, z}B,
λ
 R R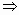 λ·b={ λ·x,
λ· y, λ·z}B
λ·b={ λ·x,
λ· y, λ·z}B
- Пусть b1|| b2, b1=
{x1, y1, z1}B,
b2={x2, y2, z2}B
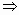
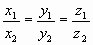 (Здесь:
(Здесь: 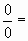 любое число). любое число).
Определение 23: Ортонормированный ( декартов ) базис – это i, j,
k, т.ч.
1) | i |=| j |=| k |=1,
2) i 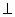 j j
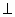 k k 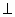 i.
i.
Замечание: i, j,
k – это стандартное обозначение именно декартова базиса.
Т.о., встречая его в тексте можно обойтись без дополнительных пояснений относительно системы координат.
Пример 2.
Доказать свойство координат коллинеарных векторов
Пример 3.
Проверка коллинеарности векторов
Пример 4.
Найти координаты середины отрезка


|

