Определение 25: Ортогональная ( декартова ) система координат это

1. единица масштаба ( отрезок, длина которого будет считаться "единичной" ),
2. фиксированная т.О ( начало координат )
3. ортонормированный базис е₁, е₂, е₃ (изменим стандартное обозначения для удобства)
4. пересекающиеся в т.О прямые l₁, l₂, l₃, т.ч. l_i содержит реализацию е_i, i=1,2,3.

Если на l_i зафиксировать "положительное" направление в соответствии с направлением е_i, получим оси координат (стандартное обозначение осей: Ox, Oy и Oz).

Теорема2: Если известны координаты точек А=(x₁,y₁,z₁) и B=(x₂,y₂,z₂) , то координаты вектора АВ можно вычислить по формуле: АВ={ x₂-x₁ , y₂-y₁ , z₂-z₁ }.

Теорема3: Если в ортогональной системе координат b={x, y, z}, то | b |=.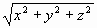

Пример 5. Разложение вектора в заданном базисе

Пример 6. Вычислить координаты векторов

Пример 7. Вычислить длины сторон треугольника