Синтаксис:

Описание:

Функция yi = spline(x, y, xi) интерполирует значения функции y в точках xi внутри области определения функции, используя кубические сплайны [1].

Функция pp = spline(x, y) возвращает pp-форму сплайна, используемую в М-файлах ppval, mkpp, unmkpp.

Функция v = ppval(pp, xx) вычисляет значение кусочно-гладкого полинома pp для значений аргумента xx.

Функция [breaks, coefs, l, k] = unmkpp(pp) возвращает характеристики кусочно гладкого полинома pp:
            breaks - вектор разбиения аргумента;
            coefs - коэффициенты кубических сплайнов;

            l = length(breaks) - 1;
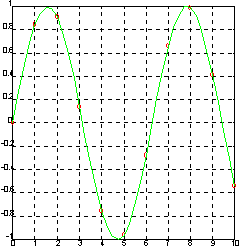
            k = length(coefs)/l.

Функция pp = mkpp(breaks, coefs) формирует кусочно-гладкий полином pp по его характеристикам.

Пример:

Зададим синусоиду всего 10 точками и проведем интерполяцию кубическими сплайнами, используя мелкую сетку.

            x = 0:10; y = sin(x);
            xi = 0:.25:10;
            yi = spline(x, y, xi);
            plot(x, y, 'o', xi, yi, ‘g’), grid

Определим pp-форму сплайна.

           pp = spline(x, y);
           [breaks, coeffs, l, k] = unmkpp(pp)
           breaks = 0   1    2   3   4   5   6   7    8   9   10
           coeffs =

          l =    10
          k =    4
Вычислим pp-форму в узловых точках сетки.

          v = ppval(pp,x)
          v =

Алгоритм:

Интерполяция сплайнами использует вспомогательные функции ppval, mkpp, unmkpp, которые образуют небольшой пакет для работы с кусочно-гладкими полиномами.

Существенно большие возможности для работы со сплайнами предо-ставляет пользователю специализированный пакет Spline Toolbox [2].

Сопутствующие функции: ICUBIC, INTERP1, POLYFIT, Spline Toolbox.

Ссылки:

1. Carl de Boor. A Practical Guide to Splines. Berlin, 1978.

2. Spline Toolbox. User’s Guide. Natick: The MathWorks, Inc., 1992.