Синтаксис:

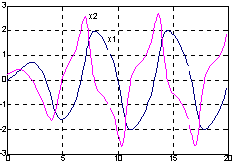
            [t, X] = ode23(‘<имя функции>‘, t0, tf, x0)
            [t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace)
            [t, X] = ode45(‘<имя функции>‘, t0, tf, x0)
            [t, X] = ode45(‘<имя функции>‘, t0, tf, x0, tol, trace)

Описание:

Функции ode23 и ode45 предназначены для численного интегрирования систем ОДУ. Они применимы как для решения простых дифференциальных уравнений, так и для моделирования сложных динамических систем.

Любая система нелинейных ОДУ может быть представлена как система дифференциальных уравнений 1-го порядка в явной форме Коши:

           ,

где x - вектор состояния;
      t - время;
      f - нелинейная вектор-функция от переменных x, t.

Функции [t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace) и [t, X] = = ode45(‘<имя функции>‘, t0, tf, x0, tol, trace) интегрируют системы ОДУ, используя формулы Рунге - Кутты соответственно 2-го и 3-го или 4-го и 5-го порядка.

Эти функции имеют следующие параметры:

Входные параметры:
‘<имя функции>‘ - строковая переменная, являющаяся именем М-файла, в котором вычисляются правые части системы ОДУ;
t0 - начальное значение времени; tfinal - конечное значение времени;
x0 - вектор начальных условий;
tol - задаваемая точность; по умолчанию для ode23 tol = 1.e-3, для ode45 tol = 1.e-6);
trace - флаг, регулирующий вывод промежуточных результатов; по умолчанию равен нулю, что подавляет вывод промежуточных результатов;

Выходные параметры:
t - текущее время;
X - двумерный массив, где каждый столбец соответствует одной переменной.

Примеры:

Рассмотрим дифференциальное уравнение 2-го порядка, известное как уравнение Ван дер Поля,

       .

Это уравнение может быть представлено в виде системы ОДУ в явной форме Коши:

Первый шаг процедуры интегрирования - это создание М-файла для вычисления правых частей ОДУ; присвоим этому файлу имя vdpol.

       function xdot = vdpol(t, x)
       xdot = [x(2); x(2) .* (1 - x(1).^2) - x(1)];

Чтобы проинтегрировать систему ОДУ, определяемых функцией vdpol в интервале времени 0 <= t <= 20, вызовем функцию ode23:

       t0 = 0; tf = 20;
       x0 = [0 0.25]'; %Начальные условия
       [t, X] = ode23('vdpol', t0, tf, x0);
       plot(t, X), grid, hold on
       gtext('x1'), gtext('x2')

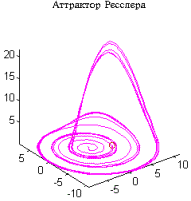
Рассмотрим простейший из известных примеров странного аттрактора - аттрактор Ресслера [1]:

где параметры {a, b, c} имеют значения {0.2 0.2 5.7}, а начальное условие задается следующим образом: x0 = [-0.7 -0.7 1].

Для того чтобы проинтегрировать эту систему в интервале времени 0<= t<= 20, вызовем функцию ode45:

        t0 = 0; tf = 20;
        x0 = [-0.7 -0.7 1]’.%Начальные условия
        [t, X] = ode45('ressler', t0, tf, x0);
        comet3(X(:, 1), X(:, 2), X(:, 3)).

Алгоритм:

Функции ode23 и ode45 реализуют методы Рунге - Кутты с автоматическим выбором шага, описанные в работе [2]. Такие алгоритмы используют тем большее количество шагов, чем медленнее изменяется функция. Поскольку функция ode45 использует формулы более высокого порядка, обычно требуется меньше шагов интегрирования и результат достигается быстрее. Для сглаживания полученных процессов можно использовать функцию interp1.

Диагностические сообщения:

Если функции ode23 и ode45 не могут выполнить интегрирование во всем заданном диапазоне времени выдается сообщение

         Singularity likely.
         Система сингулярна.

В состав версии 4.0 помимо функций ode23 и ode45 включена также функция ode23p, которая позволяет в процессе интегрирования строить в трехмерном пространстве орбиты движения для трех первых переменных состояния. Перед обращением к этой функции пользователь должен задать диапазоны изменения этих переменных, чтобы определить размер графика, используя следующие операторы:

         axis([x1min x1max x2min x2max x3min x3max]);
         hold .

Для получения тех же результатов вместо этой не столь очевидной процедуры целесообразно использовать такую последовательность:

        [t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace);
        comet3(X(:, 1), X(:, 2), X(:, 3));.

В этом случае построение орбиты реализуется автоматически, но после выполнения процедуры интегрирования. Кроме того, в данном случае пользователь может выбирать любые переменные состояния.

Для эффективного моделирования сложных динамических систем с непрерывным и дискретным временем рекомендуется использовать специализированную систему SIMULINK [3], входящую в состав программных продуктов, выпускаемых фирмой The MathWorks, Inc.

Ссылки:

1. Хакен Г. Синергетика: иерархии неустойчивостей в самоорганизующихся системах и устройствах. М.: Мир, 1985. 423 с.

2. Forsythe G. E., Malcolm M. A., Moler C. B. Computer Methods for Mathematical Computations. Prentice-Hall, 1977.

3. SIMULINK. User’s Guide. Natick: The MathWorks, Inc., 1990.