© Ф.Пинежанинов
В начало
Зеркало: http://pinega.da.ru/
Цель этой статьи изучить как деформации
конечного элемента, или другими словами смещения
точек, влияют на точность интерполяций с помощью
этого элемента. Будет использована технология
исследования, аналогичная развитой в статье
"Свойства базисных функций", правда
несколько модернизированная для сравнения
разных, но в некотором смысле, следующим из
контекста, эквивалентных между собой элементов.
Дело в том, что при вычислениях на цифровом
компьютере с конечным машинным словом, всегда
приходится иметь дело не с множеством
действительных чисел с которым обычно оперирует
математика, а с конечным подмножеством
рациональных чисел, следовательно неизбежно
возникают ошибки за счет усечения или
округления. Наиболее изучено поведение ошибок
при решении систем линейных уравнений
поэтому, будем использовать модель поведения
ошибок согласно правила, приведенного в работе
Гильберта Стренга: "Эмпирический закон,
экспериментально проверенный, состоит в том, что
при исключении Гаусса при наличии ошибок
округления в решении может потерятся log
десятичных знаков ".
По десятичному логарифму числа
обусловленности матрицы Грама в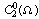 ,согласно с
эмпирическим законом, указанным Стренгом, будем
оценивать точность получения интерполируемых
величин. Будем также использавать,введенную в
статье "Свойства базисных функций" ,
гипотезу о продолжении на ,согласно с
эмпирическим законом, указанным Стренгом, будем
оценивать точность получения интерполируемых
величин. Будем также использавать,введенную в
статье "Свойства базисных функций" ,
гипотезу о продолжении на 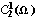 и, "по
десятичному логарифму числа обусловленности
матрицы Грама в и, "по
десятичному логарифму числа обусловленности
матрицы Грама в 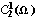 оценивать точность
получения производных от интерполируемых
величин". оценивать точность
получения производных от интерполируемых
величин".
При этом естественно предполагать, что
простое изменение масштаба сохраняет
свойства, поэтому, использование в мере
влияния неопределенности производных по x,y,z
не подходит, в силу разных размерностей у
базисных функций и их производных, поэтому
простое увеличение или уменьшение масштаба
будет приводить или к хорошей или к плохой
обусловленности системы базисных функций при
скалярном произведении включающем производные
для пространства функций С1.
Простое использование определения скалярного
произведения для С1, использованное в статье
"Свойства базисных функций" не учитывает
преобразование к производным по x,y,z, а именно их
поведение наиболее интересно с точки зрения
практических применений. Кроме того, в тех
случаях, когда якобиан постоянный, а это бывает в
случае аффинных преобразований исходного
конечного элемента, элементы будут не различимы
с точки зрения как пространства функций С0 так и
С1. Это скалярное произведение прекрасно годится
для оценки влияния отклонений
изопараметрических преобразований от аффинных
преобразований, но не отражает существа дела при
самих аффинных преобразованиях, определение
которых будет приведено позднее.
После некоторых вычислительных экспериментов
автор остановился на следующем гибриде: в
скалярном произведении для С1 используются
производные по x,y,z, умноженные на половину
длины ребра эквивалентного по объему квадрата
или куба. Другими словами коэффициент на который
надо умножить координаты исходного конечного
элемента, чтобы получить такой же обьем. Такое
определение скалярного произведения наиболее
полно отражает влияние деформаций конечного
элемента на производные и не зависит от
масштабов задачи.
Этот способ анализа свойств систем функций
хорош - он учитывает влияние как аффинных
преобразований так и параметрических
возмущений, однако когда присутствуют оба вида
деформаций и матрица Якоби достаточно сложная,
анализ становится затруднительным на доступном
автору железе и софте, поэтому для оценки влияния
параметрических возмущений в подобных ситуациях
используется более быстрый способ оценки
принятый в статье "Свойства базисных
функций", правда с учетом якобиана.
Вычисление свойств системы функций оформим в
виде нескольких процедур, для того, чтобы не
усложнять текст однообразными вставками. Также
будем оформлять и изображение элемента.

Аналогичный набор для треугольника:


Реальные конечные элементы, будут конечно
иметь гладкие кривые на сторонах, но для наших
целей достаточно и схематичного изображения в
виде ломанных, так проще и понятнее как
рисуется.

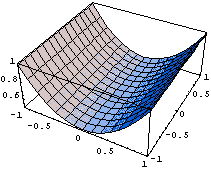
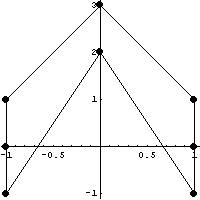
Рассмотрим типичный квадратичный элемент.
Сначала построим его базисные функции и убедимся
в эквивалентности определения введенного
скалярного произведения использованному в
статье "Свойства базисных
функций" этой серии:
Пространство C 0 Число обусловленности
= 40.3521 Теряем цифр 1.60587
Пространство C 1 Число обусловленности
= 77.1384 Теряем цифр 1.88727
так было в статье.

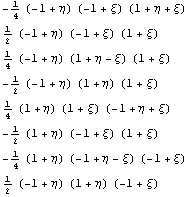

Пространство C 0 Число обусловленности
= 40.3521 Теряем цифр 1.60587
Пространство C1 Число обусловленности
= 77.1384 Теряем цифр 1.88727 D по
кси,эта
Пространство C1 Число обусловленности
= 77.1384 Теряем цифр 1.88727 D по
x,y
1
Сравнив с результатами, приведенными в начале
статьи убедимся в полном совпадении.
Сначала цитата из "Математического
энциклопедического словаря":
"Аффинное (родственное) преобразование -
точечное взаимно однозначное отображение
плоскости или пространства на себя , при котором
трем точкам, лежащим на одной прямой
соответствуют три точки, также лежащие на одной
прямой."
Аффинное преобразование является линейным и
задается формулами:
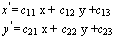 аналогично аффинное отображение задается
и в 3D пространстве.Это преобразование
образует группу, другими словами цепочка
преобразований снова образует аффинное
преобразование. С помощью этого преобразования
мы можем сжимать - растягивать, менять масштаб -
смещать, равномерно сдвигать слои конечного
элемента. Исследуем влияние изменения
степени ортогональности базисных функций
конечного элемента при воздействии на
координаты базового конечного элемента
аффинного преобразования. Посмотрим, как
влияет сжатие элемента:
аналогично аффинное отображение задается
и в 3D пространстве.Это преобразование
образует группу, другими словами цепочка
преобразований снова образует аффинное
преобразование. С помощью этого преобразования
мы можем сжимать - растягивать, менять масштаб -
смещать, равномерно сдвигать слои конечного
элемента. Исследуем влияние изменения
степени ортогональности базисных функций
конечного элемента при воздействии на
координаты базового конечного элемента
аффинного преобразования. Посмотрим, как
влияет сжатие элемента:
 =>
=> 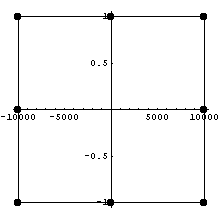
Пространство C 0 Число обусловленности
= 40.3521 Теряем цифр 1.60587
Пространство C1 Число обусловленности
= 77.1384 Теряем цифр 1.88727 D по
кси,эта
Пространство C1 Число обусловленности
= 368362 Теряем цифр 5.56627 D по
x,y
10000
Растяжение по горизонтальной варьировалось от
1 до 10000 и результаты представлены на графике, где
по горизонтали десятичный логарифм отношения
максимальной диагонали к минимальной в конечном
элементе, а по вертикали число теряемых цифр
из-за неопределенности, вносимой конечным
представлением цифр в компьютере.
 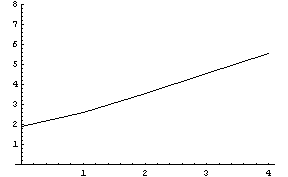
Проверим эти цифры еще для достаточно
произвольного аффинного преобразования
элемента:
 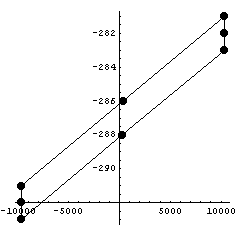
Пространство C 0 Число обусловленности
= 40.3521 Теряем цифр 1.60587
Пространство C1 Число обусловленности
= 77.1384 Теряем цифр 1.88727 D по
кси,эта
Пространство C1 Число обусловленности
= 370401 Теряем цифр 5.56867 D по
x,y
9935
Проверим еще раз на повернутом элементе, для
оценки влияния изменения углов
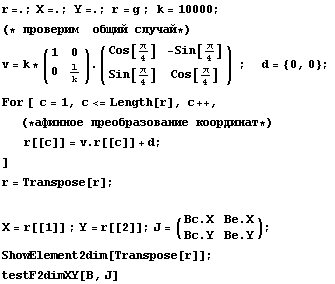
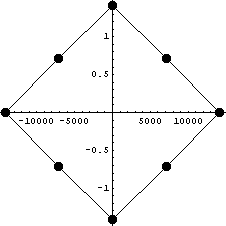
Пространство C1 Число
обусловленности = 300642 Теряем цифр
5.47805 D по x,y
10000
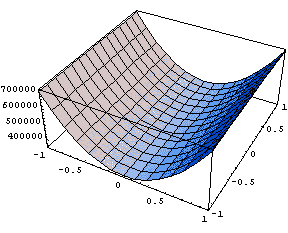
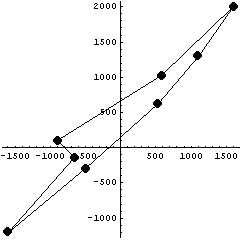
Построим соответствующий график, соединенный с
предыдущим:
 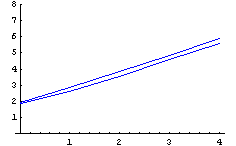
Как обычно, по горизонтальной оси
десятичный логарифм отношения максимальной
стороны прямоугольника к минимальной, а по
вертикальной число потерянных цифр в точности
конечного элемента. Повернутый на 45 градусов
конечный элемент, дает немного большие
значения.
Изменение множителя k в пределах 1, 10, 100...
до 10000 позволяет сделать вывод о том, что увеличение
пропорции между сторонами на порядок
приводит к потере примерно одной цифры
точности. Это касается тех функционалов, в
которых используются первые производные обычно
матрицы жесткости в теории упругости, а на
вычисление функционалов с базисными
функциями,обычно это матрицы масс, не
оказывается никакого влияния.
Справедлив следующий общий вывод: аффинные
преобразования геометрии конечного элемента
не влияют на вычислительные свойства его
базисных функций и производных по локальным
координатам, а меняются только свойства величин,
связанных с производными по x, y . Следуя Сьярле
конечные элементы, которые можно получить один
из другого с помощью аффинного отображения будем
называть аффинно-эквивалентными. Все
множество конечных элементов
аффинно-эквивалентных одному, называемому
базовым или исходным будем называть аффинным
семейством. Параметрические криволинейные
конечные элементы можно рассматривать, как
возмущения аффинных семейств. Еще есть вопросы,
связанные с обусловленностью матриц, но они
относятся к алгебре и их обсудим позднее.
Перейдем к оценке изопараметрических
возмущений конечных элементов.
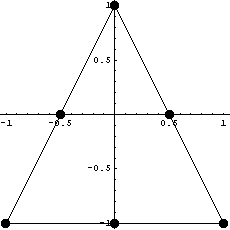
Сначала рассмотрим вариант, когда точки одной
из линий исходного элемента сливаются в одну в
центре линии

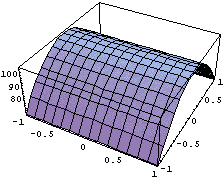
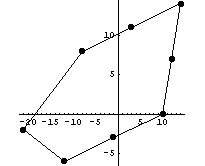
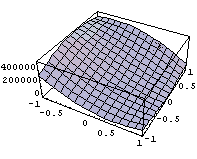
Приведен график изменения якобиана по области
элемента и его внешний вид:
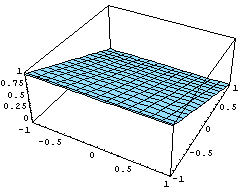 
Пространство C 0 Число обусловленности
= 125.25 Теряем цифр 2.09778
Пространство C1 Число обусловленности
= 190.5592 Теряем цифр 1.9757 D по
кси,эта
Пространство C1 Число обусловленности
= 139.106 Теряем цифр 2.14334 D по
x,y
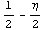 -
это якобиан преобразования области. -
это якобиан преобразования области.
Теперь уже изменяется и оценка для
функционального пространства С0
А вот для сравнения результат для
классического треугольника из статьи
"Свойства базисных функций": Пространство
C1 Число обусловленности = 721.629
Теряем цифр 2.85831. По крайней мере не хуже!
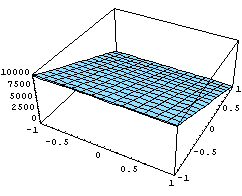
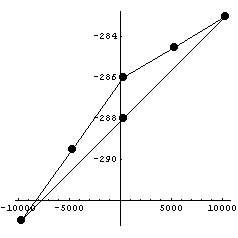
Теперь еще на этот элемент подействуем
аффинным преобразованием из предыдущего случая:

Пространство C 0 Число обусловленности
= 125.25 Теряем цифр 2.09778
Пространство C1 Число обусловленности
= 190.242 Теряем цифр 2.27931 D по
кси,эта
Пространство C1 Число обусловленности
= 87456.4 Теряем цифр 4.94179 D по
x,y
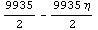
Результат аналогичен предыдущему.

Пространство C 0 Число обусловленности
= 30.4129 Теряем цифр 1.48306
Пространство C1 Число обусловленности
= 68.2514 Теряем цифр 1.82411 D по
кси,эта
Пространство C1 Число обусловленности
= 65.0367 Теряем цифр 1.81316 D по
x,y
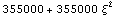
Рассмотренный выше конечный элемент близок к
квадратному, поэтому видим, что основное влияние
оказывают параметрические возмущения. Но
вычисления идут очень долго, поэтому
осуществлять анализ точности целесообразно
следующим образом, оценивать близкий аффинный
элемент по производным по x, y, оценивать влияние
параметрических возмущений по
производным по кси и эта и выбирать наибольшее.

Пространство C 0 Число обусловленности
= 49.1319 Теряем цифр 1.69136
Пространство C1 Число обусловленности =
83.2447 Теряем цифр 1.92088 D по кси,эта
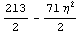
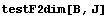
Пространство C 0 Число обусловленности
= 109.821 Теряем цифр 2.04069
Пространство C1 Число обусловленности =
228.968 Теряем цифр 2.35978 D по кси,эта
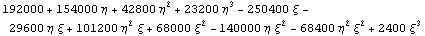

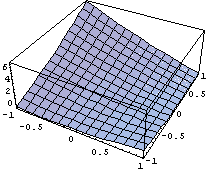
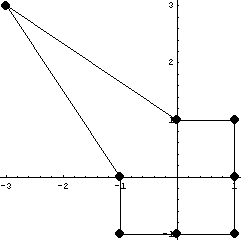
Пространство C 0 Число обусловленности
= 113.948 Теряем цифр 2.05671
Пространство C1 Число обусловленности =
191.02 Теряем цифр 2.28108 D по кси,эта
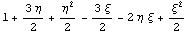

Пространство C 0 Число обусловленности
= 30.4129 Теряем цифр 1.48306
Пространство C1 Число обусловленности
= 50.0169 Теряем цифр 1.69912 D по
кси,эта
Пространство C1 Число обусловленности
= 408.1 Теряем цифр 2.61077 D по
x,y
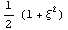
Еще один пример бочкообразного возмущения:

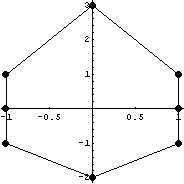
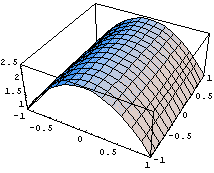
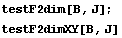
Пространство C 0 Число обусловленности
= 61.9396 Теряем цифр 1.79197
Пространство C1 Число обусловленности
= 91.3287 Теряем цифр 1.96061 D по
кси,эта
Пространство C1 Число обусловленности
= 65.9884 Теряем цифр 1.81947 D по
x,y
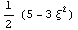
Общий вывод из последних экспериментов можно
сделать следующий: даже значительные
параметрические возмущения не приводят к
сколько - нибудь заметному возрастанию ошибки
интерполяций, основную роль в ошибке
играет аффинное преобразовение, а не
параметрическое возмущение. И на исходном и на
параметрически возмущенных конечных элементах
теряем порядка 2 цифр, что практически неощутимо
при общепринятых вычислениях с двойной
точностью.
Продемонстрируем еще это на кубично-
треугольном элементе из статьи" Метод
окаймления для простроения базисных функций
". Для этого сначала определим уравнение
линии,проходящей через 2 заданные точки:
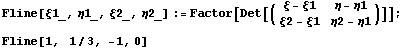 =>
=> 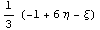
Далее опишем и изобразим исходный конечный
элемент:
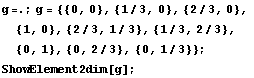
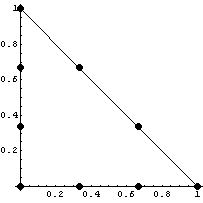
Согласно метода окаймления построим систему
исходных полиномов и трансформируем ее в систему
базисных функций конечного элемента и вычислим
соответствующие числа обусловленности:

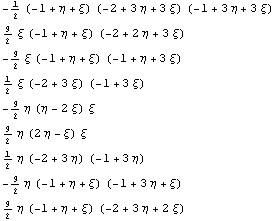
1
Пространство C 0 Число обусловленности
= 18.0674 Теряем цифр 1.25689
Пространство C1 Число обусловленности
= 1990.18 Теряем цифр 3.29889 D по
кси,эта
Пространство C1 Число обусловленности
= 1990.18 Теряем цифр 3.29889 D по
x,y
Это результаты для исходного элемента,
полностью совпадают с результатами статьи
"Свойства базисных функций".
Посмотрим, что происходит со сжатием
повернутого для симметрии элемента вращением
элемента:

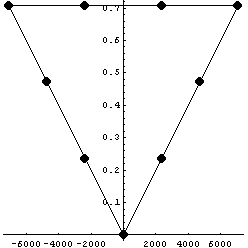
Пространство C1 Число обусловленности
= 9.89668e6 Теряем цифр 6.99549 D по x,y
Как и для квадрата будем варьировать множитель
k ={1,10,100,1000,10000}. Результаты вычислений
представлены на графике:

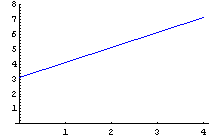
Как обычно, по горизонтальной оси десятичный
логарифм отношения максимальной стороны
треугольника к минимальной, а по вертикальной
число потерянных цифр в точности конечного
элемента.
Для трехмерных элементов немного изменим
функции с помощью которых осуществляем анализ, в
основном это касается переопределения
скаларного произведения:


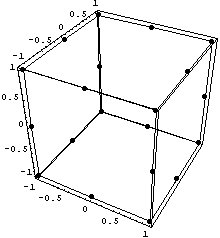
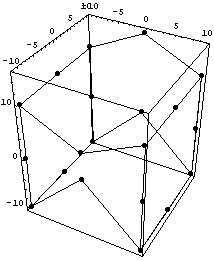
Рисование конечного элемента
осуществляется через рисование его граней. Для
программистов советую обратить внимание на
порядок перечисления узлов в грани элемента.
Этот порядок гарантирует, что нормаль к
поверхности будет направлена внутрь области при
использовании правого винта. Этого же правила
следует придерживаться и при описании области,
это избавит Вас от многих хлопот при
использовании машинной графики, обеспечит
положительность якобианов в разумных ситуациях,
упростит задание распределенных по
поверхности воздействий. Вообще обратите
внимание на согласованность правил для
ориентированных объемов, поверхностей и линий.

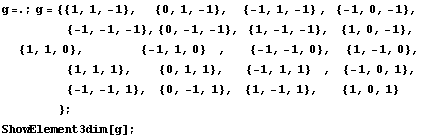
Согласно методу окаймления строим семейство
окаймляющих узлы функций:
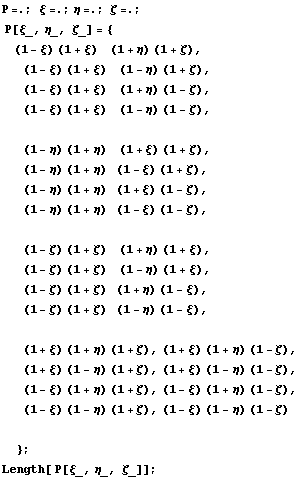
Превращаем их в семейство базисных функций:

281474976710656
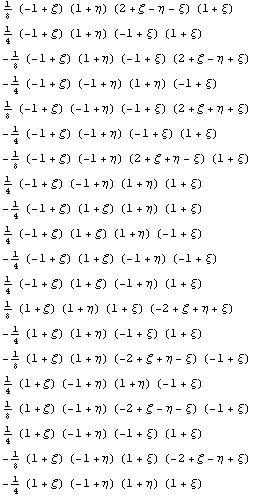
Проверяем свойства исходного элемента:
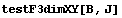
Пространство C1 Число обусловленности
= 207.733 Теряем цифр 2.31751 D по
x,y,z
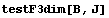
Пространство C 0 Число обусловленности
= 227.721 Теряем цифр 2.3574
Пространство C1 Число обусловленности
= 207.733 Теряем цифр 2.3574 D по
кси,эта,dzeta
Теперь посмотрим изменение свойств при
вращениях:
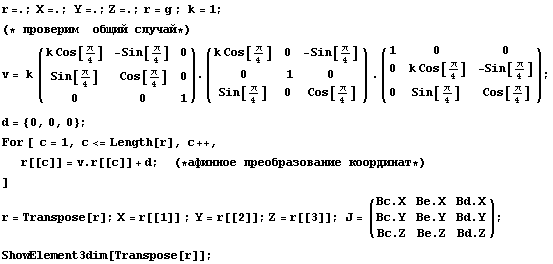
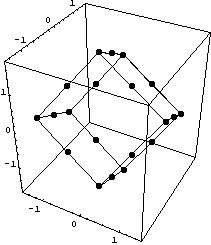
Пространство C1 Число обусловленности
= 405.122 Теряем цифр 2.60759 D по x,y,z
Исследуем изменение точности при сжатии по
одной из координат:
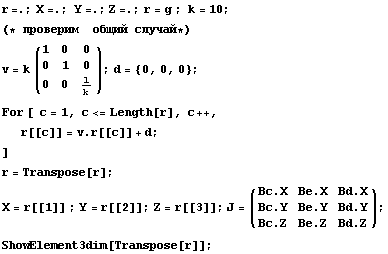
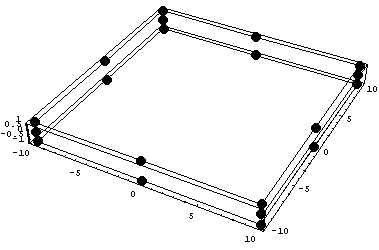
Пространство C1 Число обусловленности
= 2501.59 Теряем цифр 3.39822 D по x,y,z
Как и в предыдущих случаях варьировалась
толщина:

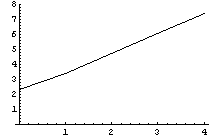
Эти результаты интересно сравнить с
результатами полученными в статье "Базисные
функции для конечных элементов с
производными" для эквивалентного
квадратичного элемента с первыми производными в
качестве степеней свободы: "Пространство C
1 Число обусловленности = 21871.3
Теряем цифр 4.33988", а ведь хорошо известно
что первых производных маловато для теории
оболочек, а если вычислим характеристики для
элементов со вторыми производными то ситуация с
точностью интерполяций только ухудшится, так как
существенно возрастут степени полиномов. При
вычислениях с двойной точностью, а это наиболее
распространенный способ сегодня, пропорции
сторон порядка 1/100 являются вполне безопасными
при решении задач об оболочках, как
трехмерных задач и по мнению автора, такой способ
является предпочтительным.
Используя гуманитарный способ доказательства,
cошлемся на мнение Сьярле: " По существу,
имеется пять типов таких аппроксимаций: 1)
Оболочка рассматривается как трехмерное тело и
соответственно используются трехмерные
изопараметрические конечные элементы... .
Добавим, что в инженерной практике этот метод в
ряде случаев конкурирует с методами,
непосредственно основанными на двумерной
постановке" . Не случайно он поставил его на
первое место.
Для трехмерного случая есть еще интересный
вариант, когда аффинное преобразование
осуществляет сжатие по двум координатам, то есть
моделирование трехмерными объектами по существу
одномерных:
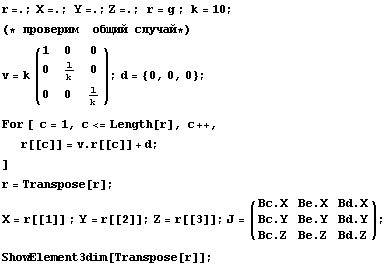 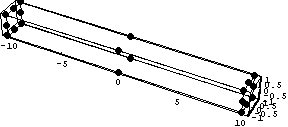
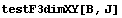
Пространство C1 Число обусловленности
= 862.007 Теряем цифр 2.93551 D по
x,y,z
10

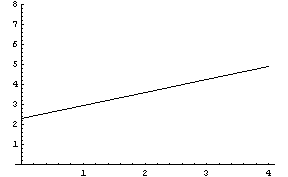
Сравнивая с результатами для деформирования
только по одному направлению видим, что ситуация
для деформирования сразу в двух направлениях
примерно в 1.2-1.4 раза лучше. Таким образом,
трехмерные элементы можно вполне уверенно
использовать для моделирования стержневых
систем.
Далее рассмотрим влияние изопараметрических
возмущений:
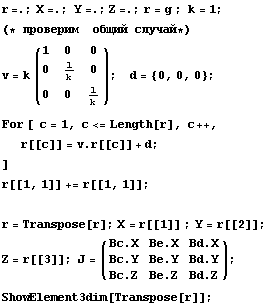
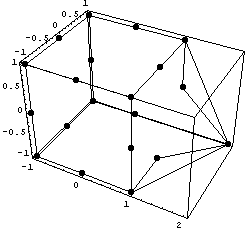
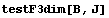
Пространство C 0 Число обусловленности
= 259.354 Теряем цифр 2.41389
Пространство C1 Число обусловленности
= 234.541 Теряем цифр 2.37022 D по
кси,эта, дзета
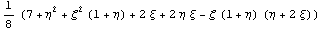
И еще один достаточно общий вариант
деформирования элемента:
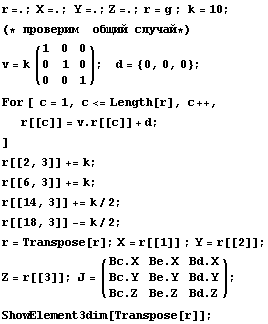
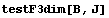
Пространство C 0 Число обусловленности
= 179.684 Теряем цифр 2.25451
Пространство C1 Число обусловленности
= 215.119 Теряем цифр 2.33268 D по
кси,эта, дзета
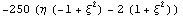
Как и в случае двумерных конечных элементов
видим, что разумные параметрические возмущения
незначительно влияют на точность интерполяций.
Вычисления занимают слишком много времени на
доступной автору вычислительной технике и
программному обеспечению, поэтому подробное
исследование свойств других элементов
рассмотренных в этой серии статей отложим до
лучших времен.
Единственно рассмотрим влияние аффинных
преобразований деформации по одному и двум
направлениям для популярных линейных
кубиков. Сначала перестроим функцию
рисования:

А теперь построим кубик:
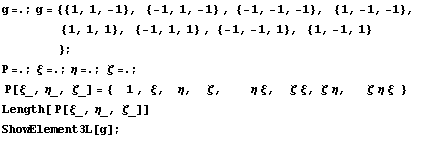
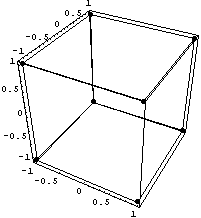
 =>
=> 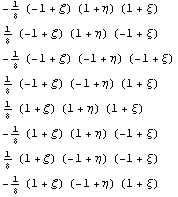
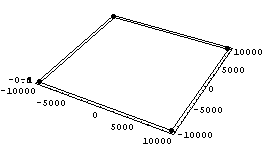
Исследуем поведение этого элемента при
аналогичных вариантах изменения:
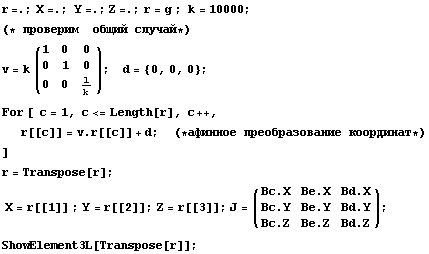
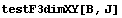
Пространство C1 Число обусловленности
= 1.93899e6 Теряем цифр 6.28758 D по
x,y,z
100000000
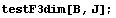
Пространство C 0 Число обусловленности
= 27 Теряем цифр 1.43136
Пространство C1 Число обусловленности
= 10 Теряем цифр 1 D по кси,эта,
дзета
Это превращение трехмерного элемента в
пластину, ситуация вполне аналогична всем
исследованым ранее и вот график:

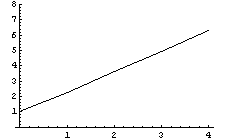
Далее как обычно превратим в балку:
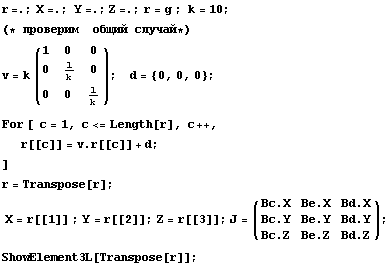
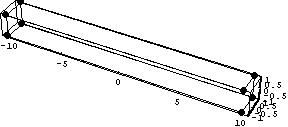
Результирующий график для этого элемента,
показывает, что эти элементы тоже можно
эффективно использовать для моделирования
стержней, и интересно сравнить с точностью,
которую мы получаем для одномерного линейного
элемента с производными, но это в следующих
статьях.

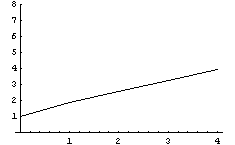 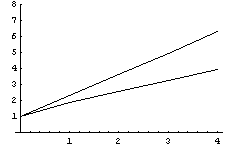
Как и ранее верхняя линия соответствует
превращению в пластинку, а нижняя в балку.
Естественно было бы исследовать еще и кубичный
элемент, но к сожалению не хватило мощности
компьютера и програмного обеспечения. Но
принципиально поведение понятно и без
этого.
При получении результатов, использовались
определения скалярного произведения по
Соболеву, принятые в математической физике, в
предметных областях функционалы выглядят
несколько иначе. Обычно базисные функции и
производные не участвуют вместе и присутствуют
не все произведения производных, а,например, в
теории упругости функционал определяется через
соотношения Коши. Поэтому на приведенные в этой
статье оценки можно смотреть как на оценки
сверху.
Внимательный читатель спросит, почему бы не
использовать в определении скалярного
произведения только производные? Дело тут в
следующем, базисные функции это n полиномов,
содержащих константу и линейный член, при
дифференцировании порядок полиномов понизится и
следовательно, набор полиномов из производных
будет линейно зависимым. Это приведет к
вырожденности матрицы Грамма и она будет
необратима, и следовательно ни о каких
собственных числах, а следовательно об
обусловленности говорить нет смысла. Отсюда
кстати следует правило для краевых условий в
функционалах, их должно быть не меньше чем надо
для того, чтобы матрица Грамма была
невырожденной. В случае 3D теории упругости
например: три производных для трех переменных
(u,v,w) , следовательно не менее 9 условий на
функционал, что в механике обычно определяют как
отсутствие перемещений как жесткого целого. Для
других задач несложно получить аналоги.
Следует иметь в виду, что в физически
осмысленных функционалах присутствуют еще
матрицы типа матрицы упругости для теории
упругости, и они тоже вносят свою лепту в ошибку.
Ниже рассмотрим матрицу упругости для
изотропного случая. И оценим влияние физических
констант: модуля упругости и коэффициента
Пуассона на точность. Для этого слегка
модернизируем функцию c помощью которой
осуществляем анализ для использования
матриц:

Построим матрицу упругости:

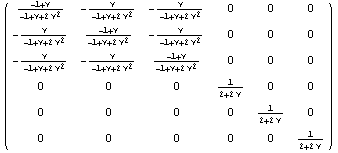
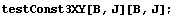
Пространство C 0 Число обусловленности
= 89401 Теряем цифр 4.95134
Столь причудливое задание матрицы Якоби и
модуля упругости использовано для того, чтобы
лишний раз подчеркнуть незавикимость
обусловленности матрицы жесткости от геометрии
элемента и от модуля упругости. Вариация
коэффициента Пуассона в пределах [0,1] позволяет
построить график, приведенный ниже.
Конечно значения коэффициента Пуассона, при
которых скорость звука будет больше физически
обоснованной беcсмысленна, а это где-то около 0.49,
но ведь занимаются и 0.5, почему бы не посмотреть,
что будет дальше? Вот результаты:

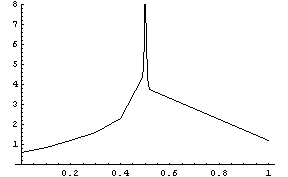
На этом графике приведено число теряемых цифр в
точности в зависимости от коэффициента Пуассона.
Как оценивать взаимное влияние матриц если
известны оценки для отдельных? Ответ на этот
вопрос дает теория возмущений. Из линейной
алгебры известны неравенства для чисел
обусловленности: cond(A)/cond(B)<= cond(AB)<=cond(A)
cond(B) (это для cond(A)>cond(B) иначе в дроби надо
поменять местами).
Прологарифмируем и получим следущую
рекомендацию : число потерянных знаков находится
между разностью и суммой. Оптимисты могут
считать, что все само собой наладится,
пессимисты, что бутерброд все равно упадет
маслом вниз. Реалистам остается думать и
экспериментировать, но, по крайней мере ,
возможный диапазон известен.
По подобной технологии можно рассмотреть
влияние и других физических характеристик.
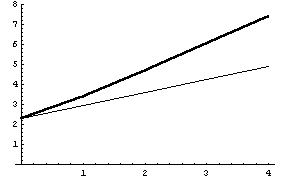
Соберем графики вместе:
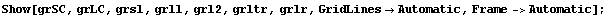
Синим цветом изображено то, что относится к
двумерным элементам, а черным к трехмерным.
Черные жирные соответствуют деформации в одном
направлении (оболочки или пластины), а черные
тонкие соответствуют переходу к стержням.
Для других элементов, которые не исследованы в
этой статье, оценки можно получить по начальной
точке, соответствущей числу теряемых цифр
исходного элемента, а угол наклона выбрать
исходя из похожего элемента, так как видим, что
для них угол наклона одинаков.
Приведем некоторые цифры по информации из MSDN:
число типа float - 7 цифр, число типа double 15 цифр, число
типа long double 19 цифр. Последний тип обычно
используется для накопления сумм, число типа
float для реальных МКЭ программ уже давно не
используется так как память стоит не дорого да и
поддержка виртуальной памяти прекрасная,
остается double -15 цифр.Тем более, что уже появляются
64 разрядные персональные компьютеры, Win-64 и можно
прогнозировать удвоение этих значений в
компиляторах для них.
Если потеряем вместо гарантированных 2-3
цифр исходного элемента вдвое больше на
построении характерных матриц, ничего страшного
не произойдет и учитывая, что матрицы как правило
положительно определенные или очень мало
отличающиеся от них, можем вполне уверенно
расчитывать на успешное решение при отношении
максимальной диагонали конечного элемента к
манимальной на 2-3 порядка. При этом желательно
чтобы изопараметрические отклонения от похожего
аффинного элемента были небольшими. Читая
старые книги, Вы увидите рекомендации как можно
меньше отклоняться от геометрии исходных
элементов и с этим можно согласиться, если
помнить, что они написаны на опыте программ,
основанных на числах типа float.
Представляется интересным исследовать
подобным образом конечные элементы с
производными и сравнить по внутренне присущим
ошибкам с трехмерными элементами. Это позволит
точнее очертить области предпочтительных
применений и области эквивалентности, в которых
использование обоих типов интерполяций дает
равносильные результаты.
В свете выше изложенного интересным
представляется рассмотрение вопроса о численном
интегрировании. Квадратурные формулы для
полиномов являются точными и всегда можно
получить оценку точности при использовании
сокращенных вариантов. Зачем считать
характеристические матрицы точно исходя из
степени подинтегральных полиномов если
достаточно укладываться в величину ошибки
внутренне присущей самой системе базисных
функций в силу отклонений от ортогональности?
Особенно актуально это для конечных элементов
с полиномами высоких степеней таких как Эрмитовы
и элементы с внутренними модами. Интересным
представляется и вопрос о естественной границе
для иерархических базисных функций: какой смысл
вводить дополнительные моды, если приращение
точности интерполяций поглотится ростом ошибок,
из-за отклонений в ортогональности системы
функций? Ответы на эти вопросы позволят
создавать сбалансированное по точности
программное обеспечение метода конечных
элементов.
Этим проблемам планируется посвятить следущие
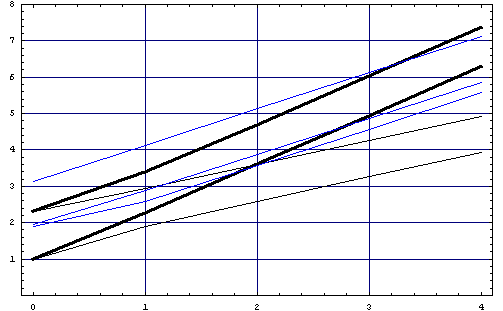
статьи этой серии, а теперь можете выпить пива из
этого нагруженного бокальчика
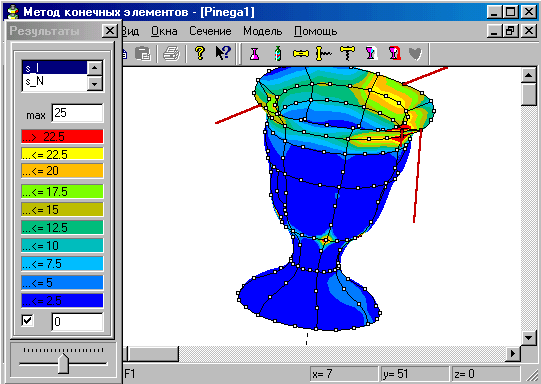
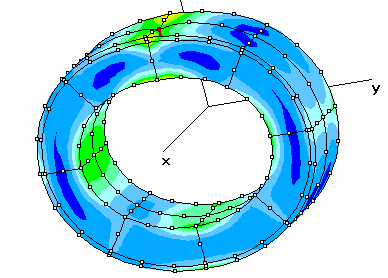
А на закуску деформированный бублик, видите
тонкий слой, ничего страшного, можно намного
тоньше, только будет плохо видно.
См. списки литературы в предыдущих статьях: 1 | 2 |
3 | 4
| 5 | 6
Санкт-Петербург, январь 2001
В начало |

