© Ф.Пинежанинов,
П.Пинежанинов
В начало
Зеркало: http://pinega.da.ru/
Исследуем возможность применения метода
окаймления для развития конечных элементов в
другом направлении: иерархических уточнениях. В
предыдущих статьях показано, как увеличивая
число узлов можно увеличивать число базисных
функций, а следовательно увеличивать точность
интерполяции. С другой стороны можно на том же
множестве узлов увеличивать число степеней
свободы за счет введения производных в качестве
неизвестных, что тоже приводит к повышению
степени полиномов, а следовательно и к повышению
точности. Во всех случаях вид базисных функций
менялся, что естественно приводит к
необходимости полного пересчета всех величин
зависящих от базисных функций. В ряде работ
предложен подход, связанный с добавлением новых
базисных функций и соответственно степеней
свободы при условии сохранения вида старых
базисных функций. Рассмотрим, как надо
модифицировать алгоритм, предложенный в
предыдущих статьях, чтобы он позволял добиваться
указанных выше целей.
Сначала немного определений и алгебры, на
которые будем опираться при дальнейших
рассуждениях.
Подпространство L линейного пространства X
называется инвариантным относительно
квадратной матрицы A если 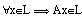 . У Воеводина и
Кузнецова приведено важное свойство - "Если
матрица A невырожденая, то A и . У Воеводина и
Кузнецова приведено важное свойство - "Если
матрица A невырожденая, то A и 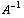 имеют одни и
те же инвариантные подпространства" другими
словами имеют одни и
те же инвариантные подпространства" другими
словами 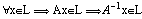 . .
В алгебре показано, что для инвариантности
подпространства необходимо и достаточно, чтобы
матрица A была полураспавшейся: то есть если
матрицу разбить двумя ортогональными линиями на
блоки, то, если мы говорим о координатах в виде
вектора-столбца, верхний внедиагональный
блок должен быть нулевым. и, согласно
приведенного свойства, такой же нулевой блок
должен быть у обратной матрицы. Факт для наших
целей очень полезный, поэтому проверим его на
примерах:
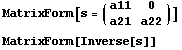 ==> ==> 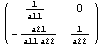 . .
Для матрицы два на два свойство соблюдается, и
можно было бы ограничиться этим, заменив деление
обращением матриц и сказав, что под a11 и так
далее подразумеваются произвольные
прямоугольные матрицы, но все- таки проверим и в
других случаях.
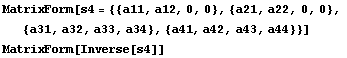 ==> ==>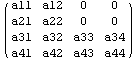 ==> Матрица ==> Матрица
Снова соблюдается и, проверим когда
внедиагональные матрицы не квадратные:
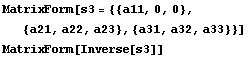 ==> ==>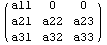 ==> ==>
 . .
И чуть иначе:
 ==> ==>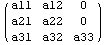 ==> ==>
 . .
Справедлив и более широкий результат:
Пусть матрица содержит пересечение нулевых
блоков, левый нижний угол каждого блока лежит
прямо над диагональю, а правый верхний совпадает
с правым верхним углом матрицы, тогда, если
матрица обратима, то структура нулевых блоков
сохранится и у обратной матрицы.
Это несложно доказать если рассматривать
нулевые блоки последовательно каждый из них даст
у обратной матрицы аналогичный нулевой блок, а
объединение даст аналогичную структуру нулевых
блоков. Проверим это на ряде модельных матриц.
 ==> ==>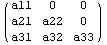 ==> ==>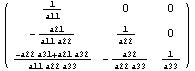 . .
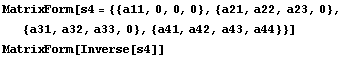 ==> ==>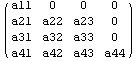 ==> Матрица ==> Матрица
Вроде можно признать, что в случае инвариантных
подпространств, структура внешних нулевых
блоков при обращении матрицы линейного
оператора сохраняется.
Вернемся к конечномерным пространствам
функций, которые, как и в предыдущих статьях
будем определять с помощью окаймляющих линий или
плоскостей, но при этом будем требовать чтобы
некоторое число функций исходного базиса
сохраняло свойство инвариантности. Другими
словами - что бы мы не добавляли к некоторому
начальному базису, его свойства, а следовательно
и вид не менялись.
В статье "Базисные функции для конечных
элементов" показано, что
конечно-элементный базис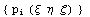 можно построить
c помощью матрицы преобразования C: можно построить
c помощью матрицы преобразования C:
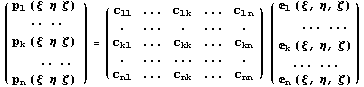
Но так как мы хотим, чтобы первые k функций
образовывали инвариантное подпространство,
другими словами не зависели от оставшихся n-k
функций, то должны потребовать, чтобы матрица C
была верхней полураспавшейся и иметь вид:
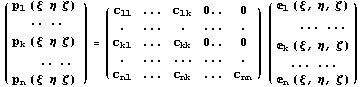 . .
Вычисляя значения функций в n узлах конечного
элемента, переходим к матричному уравнению:
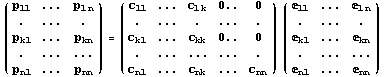 . .
Запишем решение матричного уравнения P=CE с
учетом того, что P - матрица значений базисных
функций единичная, как С= 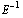 . В силу ранее
рассмотренного свойства полураспавшихся матриц,
E тоже будет полураспавшейся. Уфф... теперь уже
близко. Теперь посмотрим с другой стороны:
матрица C - это матрица неопределенных
коэффициентов и определяется на основе E,
следовательно если мы построим E как обычно, а
затем обнулим в силу требования инвариантности
верхнюю внедиагональную клетку то получим
матрицу . В силу ранее
рассмотренного свойства полураспавшихся матриц,
E тоже будет полураспавшейся. Уфф... теперь уже
близко. Теперь посмотрим с другой стороны:
матрица C - это матрица неопределенных
коэффициентов и определяется на основе E,
следовательно если мы построим E как обычно, а
затем обнулим в силу требования инвариантности
верхнюю внедиагональную клетку то получим
матрицу 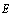 , обращение этой матрицы и даст
нам искомую верхнюю полураспавшуюся матрицу
преобразования, которая даст нам
иерархические базисные функции. , обращение этой матрицы и даст
нам искомую верхнюю полураспавшуюся матрицу
преобразования, которая даст нам
иерархические базисные функции.
Эта технология естественно урезает исходное
конечномерное пространство функций { 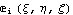 }
, но, то что останется все равно будет богаче чем
просто сокращенный набор функций. Тем более что
таким образом мы можем добавлять сколько угодно
степеней свободы. }
, но, то что останется все равно будет богаче чем
просто сокращенный набор функций. Тем более что
таким образом мы можем добавлять сколько угодно
степеней свободы.
Этот результат несложно распространить и на
семейство вложенных инвариантных
подпространств.
Полученные иерархические базисные функции
будут принимать нулевые значения в основных
узлах конечного элемента, то есть на границе
элемента, а следовательно не будут влиять на
стыковку элементов и их можно ортогонализовать в
смысле какого-либо скалярного произведения
для улучшения вычислительных свойств и
увеличения разреженности, получаемых матриц, но
об этом поподробнее расскажу позднее.
Сначала подключим возможности
ортогонализации: 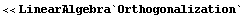
В качестве дополнительных условий используем
значения функции и ее производных в нулевой
точке, хотя можно и в любых других внутренних
точках.
Для получения иерархических функций, будем
принудительно обнулять три верхних
внедиагональных блока, что соответствует трем
вложенным инвариантным подпространствам
базисных функций, хотя можно и один или два и,
заодно, продемонстрируем ортогонализацию
добавленных иерархических функций:

336960 1
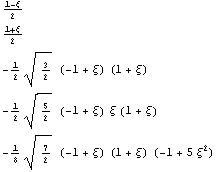 ==> ==>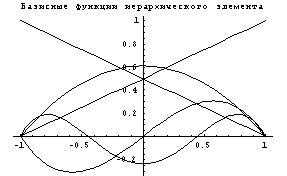 . .
Из графиков видно, что предложенная технология
построения вложенных инвариантных
подпространств функций или иерархических
конечных элементов прекрасно работает в этом
случае.
Сначала рассмотрим применение предлагаемого
метода построения иерархических конечных
элементов на линейном квадрате. Дополнительные
функции исходного базиса будем строить,
используя метод окаймления линиями точки в
начале координат так, чтобы обнулять границу,
примерно так, как это делали для элементов с
производными, то есть, используя степени линий.
В качестве дополнительных условий будем
требовать ненулевого значения и двух первых
производных в этой точке. В качестве примера
ортогонализуем иерархические базисные функции в
смысле достаточно произвольного скалярного
произведения. Разумный выбор скалярного
произведения зависит от функционала, то есть от
задачи, которую надо решать и поэтому выходит за
рамки этой статьи:

{{-1,-1}, {1,-1},{1,1},{-1,1},{0,0}}

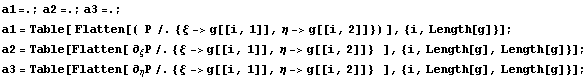
 после обнуления верхнего
внедиагонального: после обнуления верхнего
внедиагонального:  . .
-256
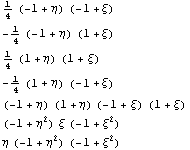 и после ортогонализации и после ортогонализации 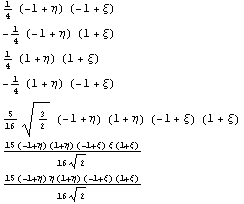
Вид функции в одном из узлов: 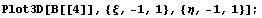
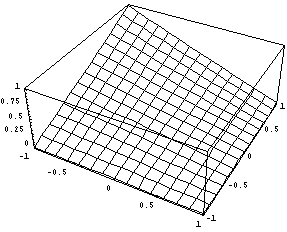
Первые четыре базисные функции совпадают с
функциями для обычного линейного квадрата, а вот
вид трех дополнительных иерархических
функций:
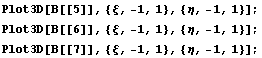
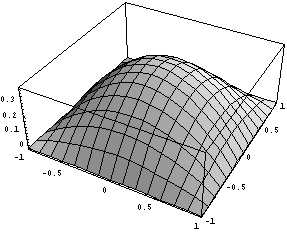
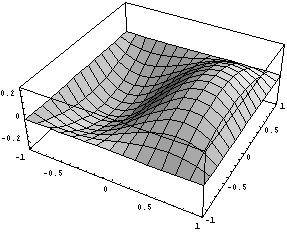
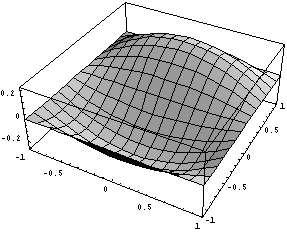
Очевидно, что для этого элемента технология
прекрасно работает и количество дополнительных
функций можно наращивать практически
неограничено. Далее аналогично рассмотрим
квадратичный элемент:

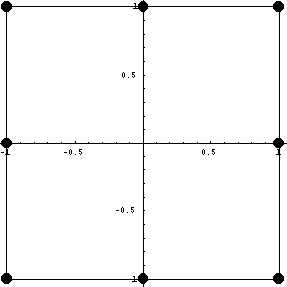
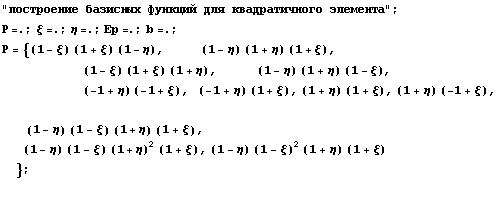
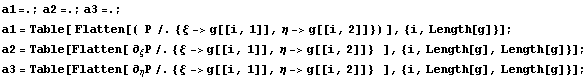

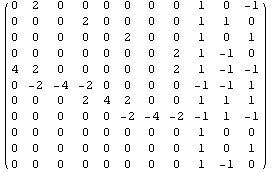 модифицируем в модифицируем в 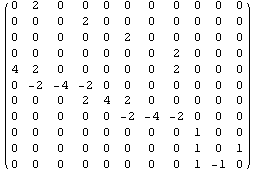 . .
4086.
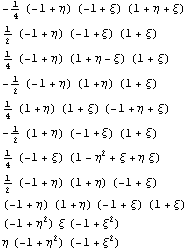 ортогонализуем ортогонализуем 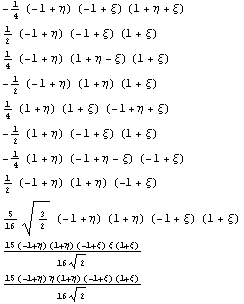
и нарисуем 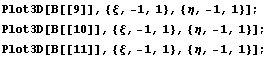
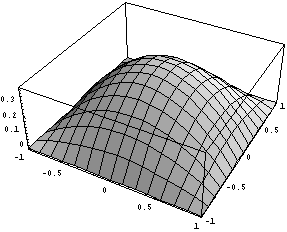
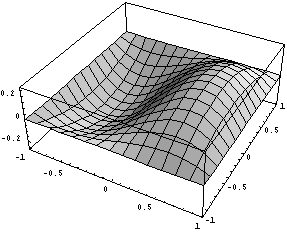
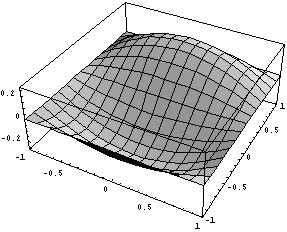
Для квадратичного элемента все тоже прекрасно
получилось. Сделаем важное наблюдение -
дополнительные иерархические базисные функции
для линейных и квадратичных элементов
получились одинаковыми. Если это свойство
присуще всем элементам узлы которых находятся на
одинаковых фигурах, то это существенно упрощает
отыскание и программирование иерархических
базисных функций. Достаточно сделать один-два
модуля и точность интерполяций можно повышать
для всех эквивалентных элементов.
Дело в том, что дополнительные функции
исходного базиса, выбираемые по методу
окаймления, обнуляют границу элемента, а нижняя
внедиагональная клетка обращаемой матрицы -
суть значения основного исходного базиса в
узлах, то есть на границе, и в силу этого нижняя
внедиагональная клетка нулевая. С учетом
требования инвариантности подпространства
основных базисных функций, матрица
преобразования оказывается распавшейся
матрицей - ненулевые только диагональные
клеточные матрицы. Это возможно только если
итоговое пространство основных и иерархических
функций образуют прямую сумму подпространств, то
есть могут рассматриваться отдельно, а
следовательно основные и иерархические
функции могут быть получены отдельно, а с
другой стороны иерархические базисные функции
будут одинаковыми для всех элементов, узлы
которых лежат на одинаковой границе.Проверим это
еще на кубических элементах.

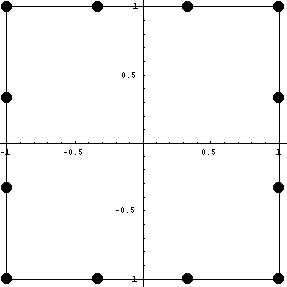

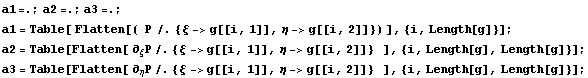


255135. 1
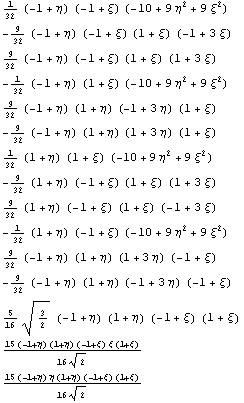

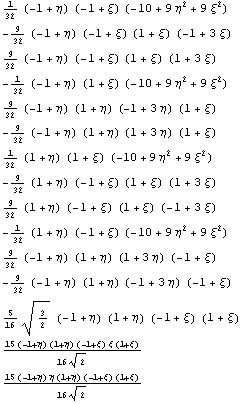
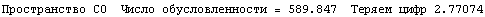

Да это свойство подтвердилось. Основные
базисные функции совпадают с функциями,
полученными в предыдущих статьях. Для
треугольных элементов не будем проверять, а
займемся трехмерными элементами и на
треугольных призмах проверим.
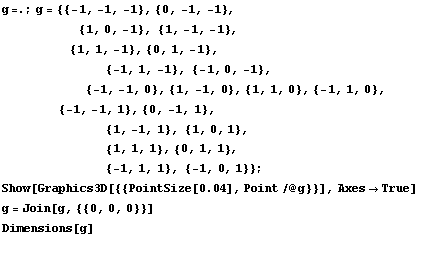
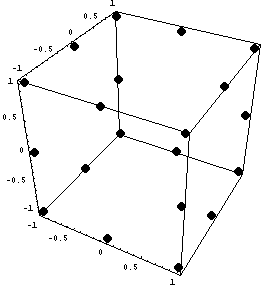
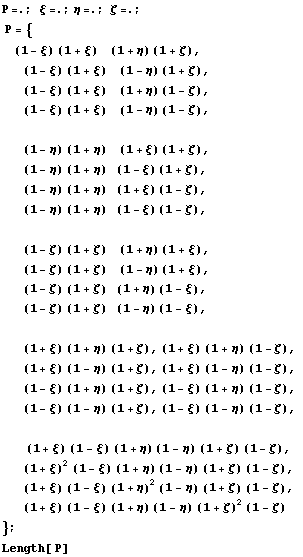
24

{24,24}

-2.81475e14 1
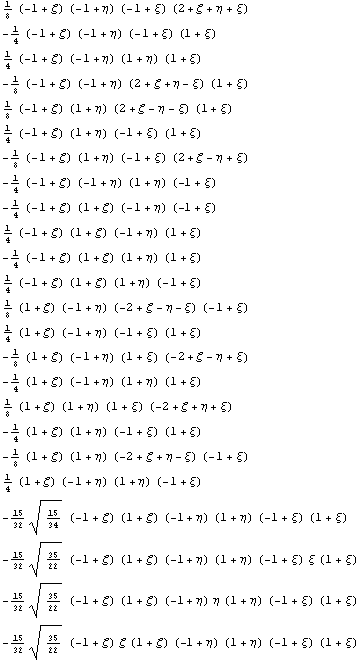
Теперь с учетом замечания о прямой сумме
подпространств, получим иерархические функции
для всех конечных элементов, узлы которых лежат
на сфере, определяемой по бесконечной норме, или
проще кубике:
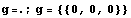 {{0,0,0}} {{0,0,0}}
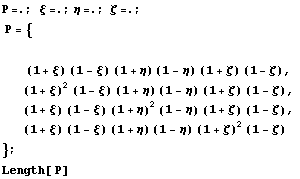
4

{4,4}

1
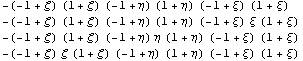
Ортогонализованные функции
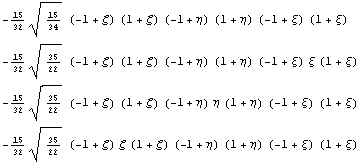
Итак, из сравнения с результатами для
квадратичного элемента, видим, что все
рассуждения о инвариантных подпространствах и
прямых суммах справедливы и получим еще
иерархических функций для скалярного
произведения, определяемого через производные:
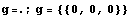

10

{10,10}


8
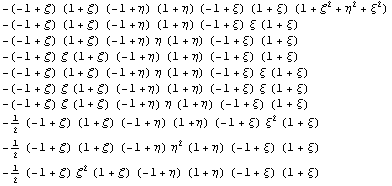
Ортогонализуем
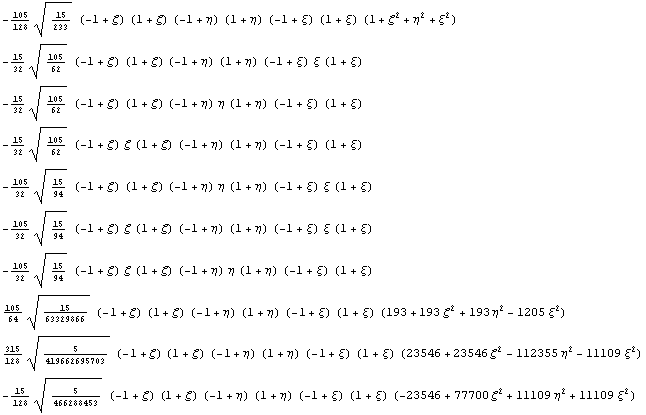
Покажем, как сделать, чтобы иерархические
функции содержали инвариантные
подпространства внутри, это удобно, так как
позволяет добавлять их не все сразу, а
постепенно, на основе анализа решений
предыдущего шага, просто окаймляя матрицу
квадратичного функционала:
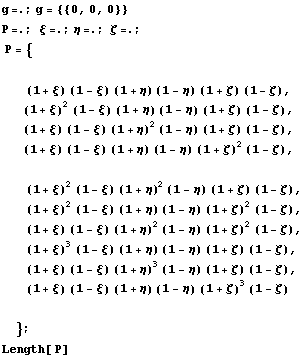
10

{ 10,10 }


-16
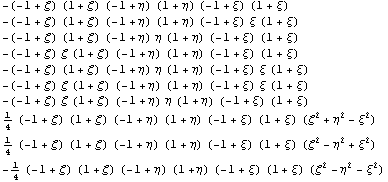
Ортогонализуем
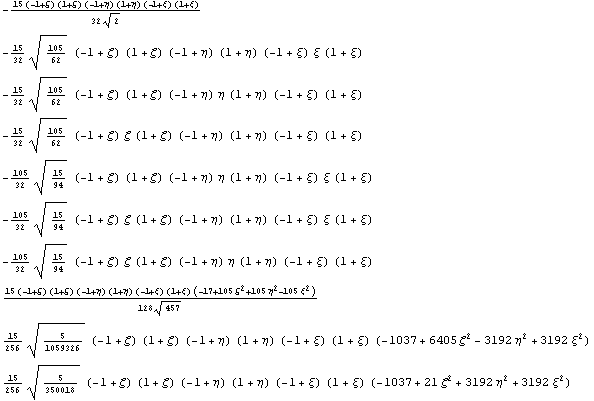
График поведения иерархической функции,
соответствующей P:
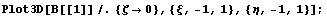
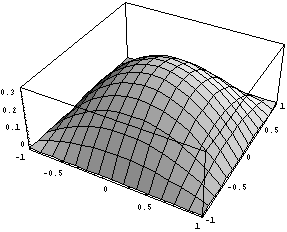
График поведения иерархической функции,
соответствующей 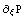 : :
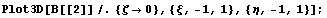
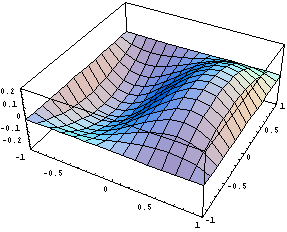
График поведения иерархической функции,
соответствующей 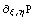 : :
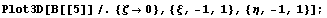
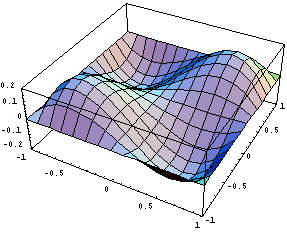
График поведения иерархической функции
полученной на основе 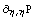 : :
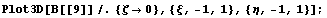
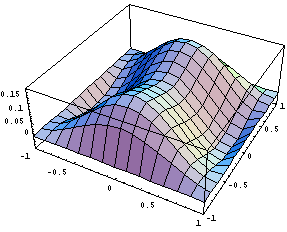
Проделаем аналогичное действие с трехмерными
треугольными призмами, производные для
симметрии будем определять в центре тяжести:
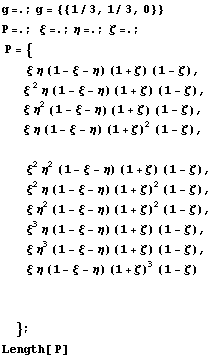
10

{10,10}


-1.16566e-13
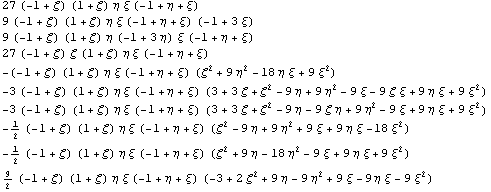
Привожу только часть ортогонализированного
базиса, остальные элементы имеют слишком
громозкое выражение:
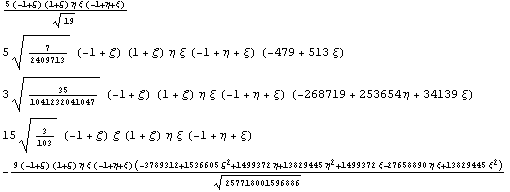
………………………..
Вычислим численные значения для полученных
функций:
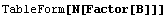
Порядки не очень хорошие и видимо не стоит
использовать. Как обычно немного порисуем в
сечении, чтобы представлять характер поведения
функций:
Расчет
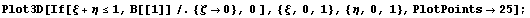
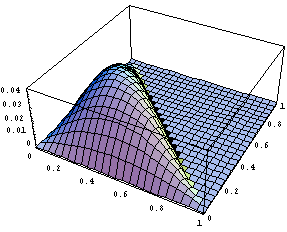
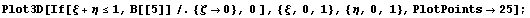
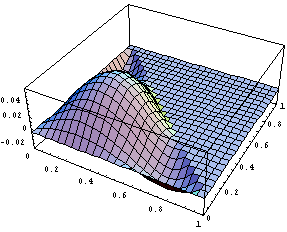
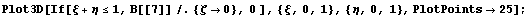
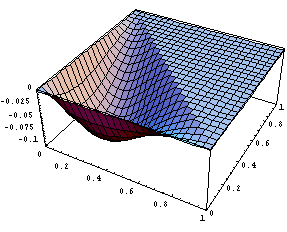
При построении иерархических функций в
качестве условий использовались производные.
Это делалось просто из подражания формуле
Тейлора и вовсе не является обязательным. Можно,
например использовать значения в точках
интегрирования по Гауссу-Лежандру или еще,
что-либо осмысленное и симметричное. В качестве
исходного базиса тоже необязательно
использовать полиномы, например подойдет
произведение тригонометрических функций,
которое обнуляет границу элемента. Но эти
вопросы еще требуют дополнительного
исследования, проводить которое сейчас у автора
нет никакого желания...
Основываясь на обычных сирендиповых элементах
можно построить дополнительные базисные
функции, как прямую сумму конечномерных
подпространств функций.
Факт прямой суммы и то, что дополнительные
степени свободы связаны только с одним узлом,
важен по следующим причинам:
- Для различных, эквивалентных по геометрии
элементов, дополнительные степени свободы
вычисляются одинаково, что очень полезно при
программировании;
- Процесс вычисления матриц для квадратичной
формы МКЭ можно разбить на несколько
последовательных этапов: сначала все вычислить
для обычных базисных функций и найти решение,
потом добавлять уточнения на основе
иерархических базисных функций. Если в
глобальной матрице степени свободы добавлять в
конце, и использовать разложение Холесского в
форме метода окаймления, как описано в книге
Джорджа и Лю, то понадобиться совсем немного
дополнительных вычислений для получения
уточненного решения. Это же касается и
итерационных методов, так как уже быдем иметь
хорошее приближение;
- Наличие нескольких последовательных решений
позволяет оценить точность на основе критерия,
подобного критерию сходимости Коши для
последовательностей.
- Несколько приближений и оценка норм их
разностей на предмет убывания ошибки позволяет
судить о качестве вычислительного процесса;
- Используя подходящую иерархическую базисную
функцию несложно наделить специальным свойством
элемент, используемый для расчета предельных
случаев, например, добавить к одному из
направлений кубическую моду для трехмерных
элементов при моделировании ими оболочек. При
этом полезно учесть, что иерархические степени
свободы можно исключить, используя
процедуру,называемую конденсация на
граничные узлы внутренних степеней свободы. Эта
процедура связана с построением матриц
квадратичного функционала и об этом подробно
поговорим в следующих статьях.
Общий вывод наверное можно сделать такой - МКЭ (
FEM - Finite Element Method ) программы стоит дополнять
иерархическими функциями, так как это несложно
сделать, не требует крупных переделок ранее
написанного кода, а выгоды существенные.
Автор надеется еще вернуться к этим вопросам в
следующих статьях и будет рад обсудить эти
вопросы с заинтересованными коллегами.
- Воеводин В.В.,Кузнецов Ю.А. Матрицы и
вычисления.-М.: Наука,1984.
- Джордж А., Лю Дж. Численное решение
больших разреженных систем уравнений.-М.: Мир, 1984.
- Зенкевич О.,Морган К. Конечные элементы
и аппроксимация:Пер.с англ.-М.: Мир,1986.
Санкт-Петербург, май 2000 года
В начало |

