© Ф.Пинежанинов,
П.Пинежанинов
В начало
Зеркало: http://pinega.da.ru/
В статье "Метод окаймления для
построения базисных функций" предложен
способ построения конечномерных пространств
функций, который позволяет построить базисные
функции для различных конечных элементов с
непрерывностью в узлах элементов.
В задачах теории пластин, оболочек и некоторых
других в результате предельного перехода в одном
из направлений возникают функционалы со вторыми
производными и искать решения надо в классах
функций с непрерывной первой производной по
крайней мере.
Как отмечается у Партона и Перлина для
дифференциальных уравнений порядка 2m должно
быть m-1 непрерывных производных.
Подробное обсуждение требований к
гладкости базисных функций или, другими
словами числу производных в качестве степеней
свободы в узлах, можно найти у Зенкевича,
где отмечается: " Здесь условие непрерывности
смешанной производной в нескольких
ортогональных направлениях фактически требует
задания всех вторых производных в такой узловой
точке ". То есть в качестве степеней свободы в
узловых точках можно требовать функций, первых
производных и вторых производных, а на серединах
сторон только функций и первых производных. Это
не очень удобно при программировании -
узлы будут иметь разное число степеней
свободы.
Цель этой статьи показать как с помощью метода
окаймления плоскостями строить подходящие
конечномерные пространства функций и находить
конечно-элементные базисные функции, при
необходимости имеющие нули второго и третьего
порядка на границах элемента и ,соответственно,
базисные функции для производных первого и
второго порядков согласованные с этими
функциями.
Ранее в статье "Базисные функции для
конечных элементов" приведено определение
конечного элемента как тройки семейств и правила
вычисления –
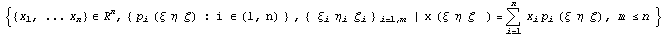 , ,
где 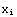 - степени свободы, - степени свободы, 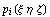 -
базисные функции, -
базисные функции, 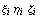 - узлы,
определяющие геометрию конечного элемента, и
считалось m=n, то обычно понималось, что число
базисных функций и число точек, определяющих
геометрию элемента, совпадают. Записывая
базисные функции - узлы,
определяющие геометрию конечного элемента, и
считалось m=n, то обычно понималось, что число
базисных функций и число точек, определяющих
геометрию элемента, совпадают. Записывая
базисные функции
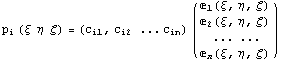 через исходный базис
пространства и, опираясь на знание их значений в
j-узлах через исходный базис
пространства и, опираясь на знание их значений в
j-узлах 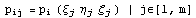 , мы получали уравнение для
квадратных матриц P=C E из решения которого,
находили неизвестные коэффициенты C
конечно-элементного базиса в исходном базисе, а
следовательно и сами базисные функции. При этом
принимается, что P – единичная матрица. , мы получали уравнение для
квадратных матриц P=C E из решения которого,
находили неизвестные коэффициенты C
конечно-элементного базиса в исходном базисе, а
следовательно и сами базисные функции. При этом
принимается, что P – единичная матрица.
Пусть m<n, то есть узлов меньше чем степеней
свободы, или эквивалентно, размерность исходного
базиса больше числа узлов, тогда P и E будут
прямоугольными матрицами и, для разрешимости
уравнений, мы должны доопределить n-m
соотношениями. Если нам известны n-m значений
некоторых производных в узлах, то,
продифференцировав выражение для 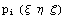 по по 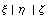 или
направлению, получим соотношения для
доопределения до квадратных матриц, а
следовательно и для определения базисных
функций, учитывающих информацию о производных.
Для примера, пусть известна информация о
производных по или
направлению, получим соотношения для
доопределения до квадратных матриц, а
следовательно и для определения базисных
функций, учитывающих информацию о производных.
Для примера, пусть известна информация о
производных по 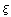 в узлах в узлах 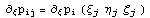 , тогда , тогда
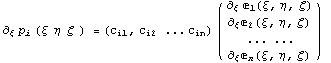 . .
Так если известна информация о соответствующих
производных во всех узлах, то получим
классические Эрмитовы конечные элементы.
Определение для двухпараметрических Эрмитовых
конечных элементов можно записать в следующем
виде:
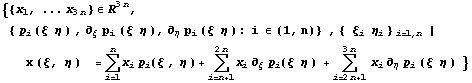 . .
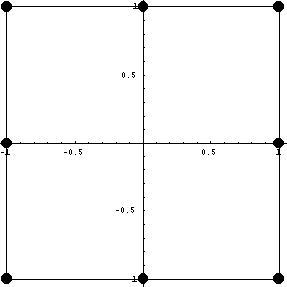
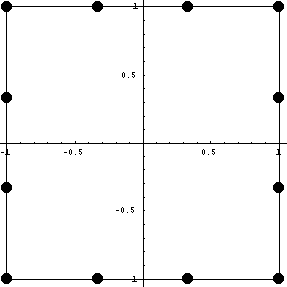
Сначала рассмотрим построение базисных
функций для квадрата с узлами в углах и функциями
и первыми производными в качестве параметров
линейной формы или правила вычисления. В
качестве исходного базиса сначала используем
обычный полиномиальный:

Сначала построим прямоугольные матрицы, где по
строкам значения исходных функций или их
производных в узлах элемента, надо-то по
столбцам, но так удобнее строить с точки зрения
программы Mathematica:
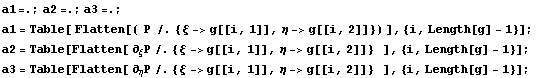
Построим общую квадратную матрицу как
объединение, транспонируем, вычислим
определитель, построим конечно-элементный базис
и проверим, что базисные функции для самой
величины являются разложением единицы:

-1.04858 e6
1
Теперь попробуем построить этот же базис
используя метод окаймления линиями. Но так как
нам необходимы полиномы более высоких степеней,
то будем добавлять степени линий так, чтобы не
нарушалась полнота исходного базиса, то есть не
было пропущено степеней линий.
Порядок степени до которого надо добавлять
члены легко определить из одномерного случая,
т.к. сужение на границу должно давать одномерный
Эрмитов элемент, а для него всегда легко
построить базисные функции используя в качестве
исходного обычный полиномиальный базис. В
рассматриваемом случае это 3,1 или 1,3. Исходный
базис строим используя окаймление двояко: сами
множители окаймляют соответствующий узел с
одной стороны, а с другой исходный базис для
элемента без производных окаймляется
аналогичным со степенями линий, а степени линий
определяются из одномерного случая.

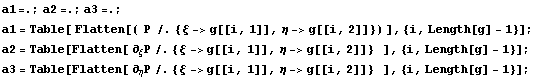

3.47892 e11
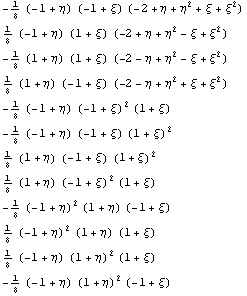
1
{0,0,0,0,0,0,0,0,0,0,0,0}
Последний вектор из нулей показывает, что
получили то же самое, что и при использовании
полиномиального исходного базиса.
Правило построения исходного базиса
достаточно просто, но, пришлось
поэкспериментировать, пока его удалось
установить.
Строить конечно-элементные базисы для
элементов с производными, опираясь на исходный
полиномиальный, не удается в силу причин
указанных в предыдущих статьях, поэтому для
дальнейших построений будем использовать
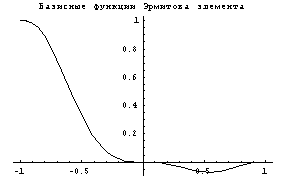
окаймляющий подход. Посмотрим как выглядят
функции:
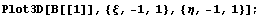
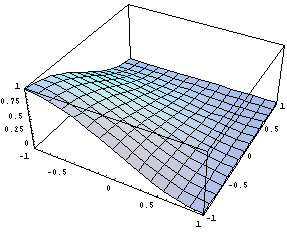
А это уже график функции для производной:
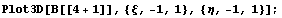
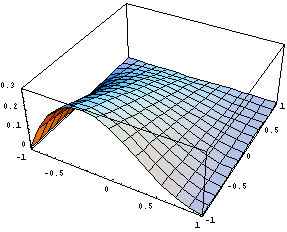
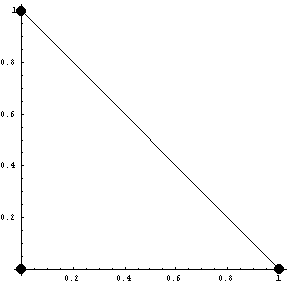
Проделаем аналогичное с линейным
треугольником. Сначала с полиномиальным базисом:

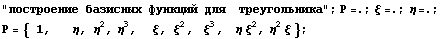

{9,9}
-1.
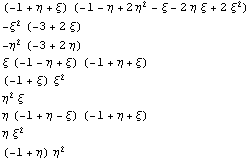
1
Теперь используя метод окаймления, понимаемый
уже в более широком смысле, описанном выше и так
как противоположная сторона одна будем
использовать ее степени для построения
исходного базиса :

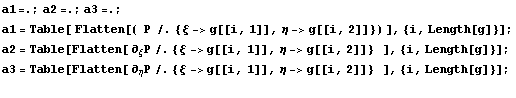
{9,9}
1
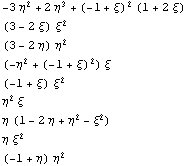
1
{0,0,0,0,0,0,0,0,0}
Хотя функции выглядят не симметричными
относительно переменных, на самом деле это не так
в чем легко убедиться простым раскрытием скобок.
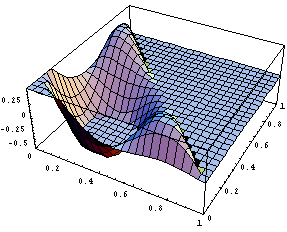
Построим некоторые графики над треугольником,
а отсечение лишнего осуществим с помощью
логического условия:
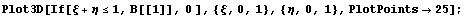
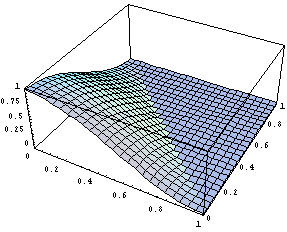
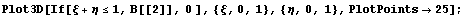
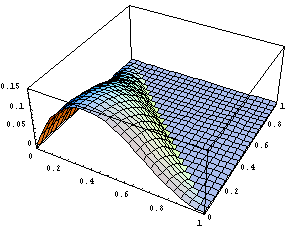
Снова видим, что оба подхода дают одинаковые
результаты. График функции выглядит прекрасно и
видно, что в угле производная равна нулю. Далее
попробуем применить метод окаймления к
элементам с более высоким порядком точности.
Рассмотрим обычный квадратичный элемент.

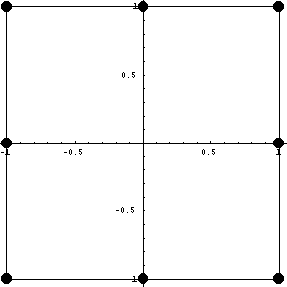
Раздельно будем прописывать углы и стороны:

{24}

1.72938 e19
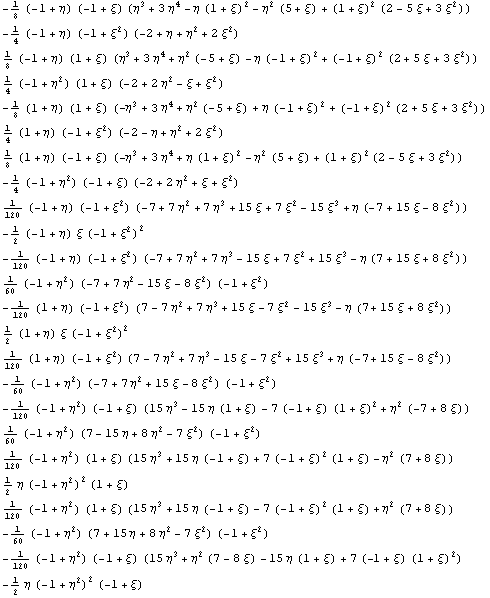
1
Комбинация степеней 1 и 4 является наименьшей,
так как любое снижение приводит к нулевому
определителю.Простыми экспериментами
проверялось, что 4 1 и 1 4 дают одинаковые
результаты.
Нарисуем несколько картинок, дающих
представление о поведении функций:
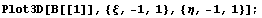
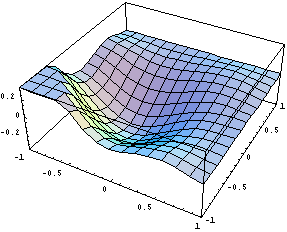
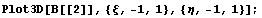
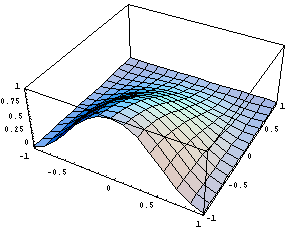
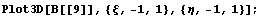
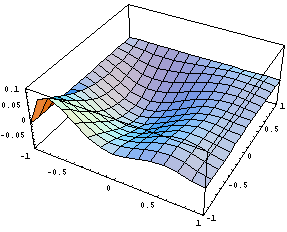
Исследуем вычислительные свойства с точки
зрения технологии, предложенной в статье
"Свойства базисных функций":

Пространство С0 Число обусловленности =
14919.8 Теряем цифр 4.17376
Пространство С1 Число обусловленности =
21871.3 Теряем цифр 4.33988
Рассмотрим обычный кубичный элемент с первыми
производными в качестве степеней свободы. Для
удобства сделаем функцию для прямой линии,
проходящей через две, заданные точки:
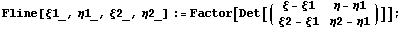

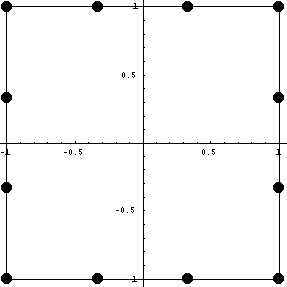

{36}
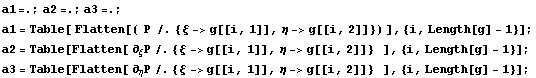
5.90363 e28

5.90363 e28
Расчет
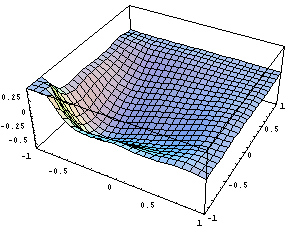
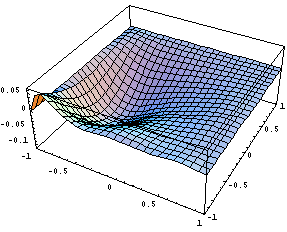
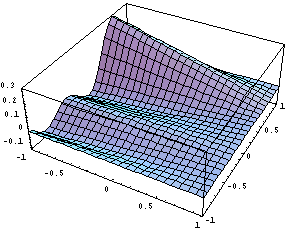
Хотя функции получились довольно громозкими,
они являются разложением единицы и
геометрически выглядят неплохо:
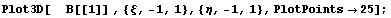
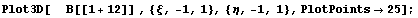
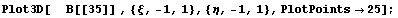

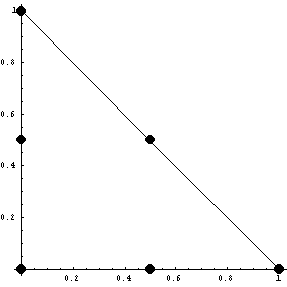
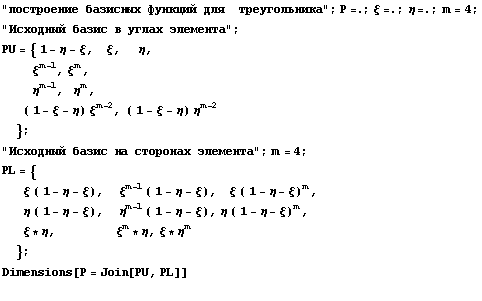
{18}
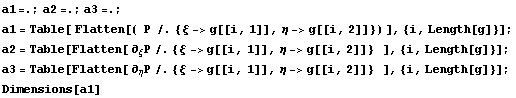
{6,18}

{18,18}
2.32831e-10
Расчет
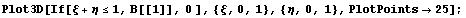
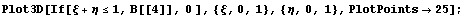
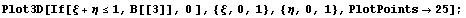
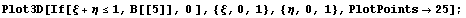
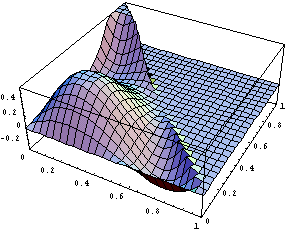
Сначала определим необходимый порядок
полиномов для линейного одномерного случая,
имеем 2 узла по 3 степени свободы в каждом,
следовательно надо иметь пятую степень
полиномов

-2048
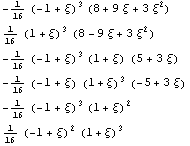
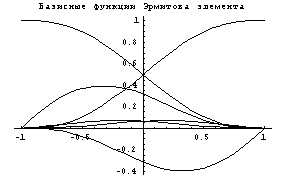
Далее построим для двухпараметрического
семейства:
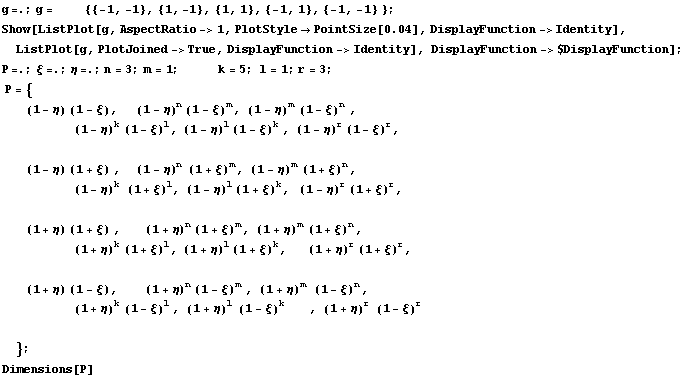
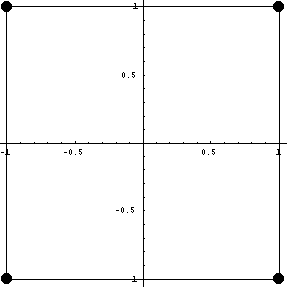
{24}

{24,24}
1.26908e33

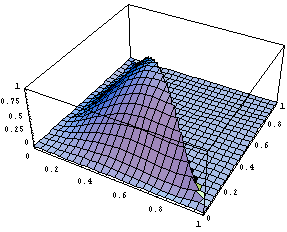
Вид функции в 1 узле: 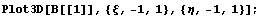
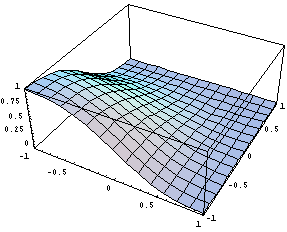
Вид одной из первых производных в первом узле:
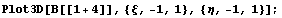
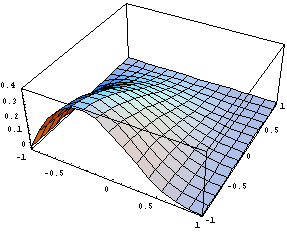
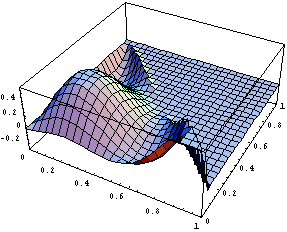
Вид одной из вторых производных в первом узле:
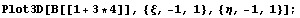
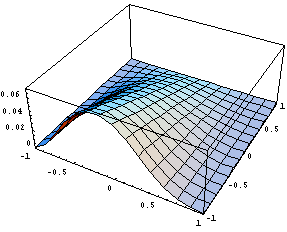
Интересно посмотреть вычислительные свойства
этой системы базисных функций, относительно
принятой в статьях технологии:

Пространство С0 Число обусловленности =
594836 Теряем цифр 5.7744
Пространство С1 Число обусловленности =
157195 Теряем цифр 5.19644
Построим базисные функции для квадратичного
элемента со вторыми производными.
Сначала оценим для одномерного квадратичного
элемента - для него исходный базис должен
содержать 9 функций:

-4096
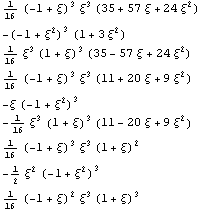
1
Максимальный порядок должен быть 8 по каждой
переменной, чтобы сужение на линию давало
одномерный случай, и еще надо добавить по 3
функции для каждого узла, чтобы была возможность
конструировать для вторых производных. Как
обычно будем использовать степени линий
окаймляющих соответствующий узел:

{48}
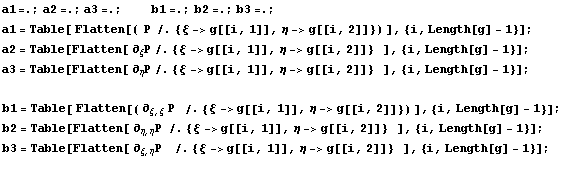

{48,48}
2.37943e58
Расчет
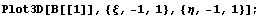
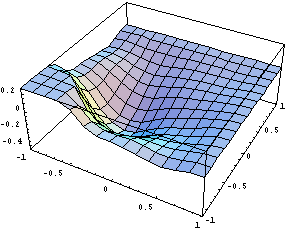
Простым сравнением выражений несложно
убедиться, что сужение на границы совпадает с
одномерным случаем.
Далее рассмотрим кубичный элемент. Сначала как
обычно одномерный случай кубичного элемента со
вторыми производными включительно

{12,12}
25.5754

1

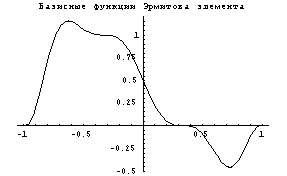
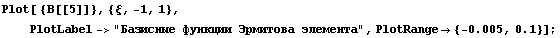
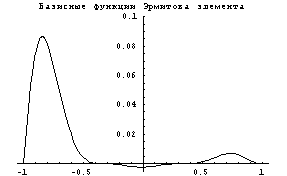
Вид у функций и производных трудно назвать
изящным, но похоже на правду. Теперь приступим к
двухпараметрическим элементам, опираясь как
обычно на метод окаймления и степени окаймляющих
линий:
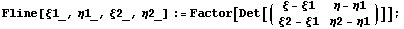


{72}
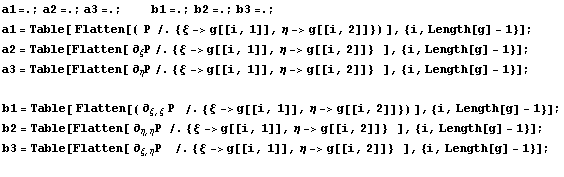

{72,72}
1.22607e92
Функций не привожу, так как буфер обмена не
справился, если кому-то надо вычислите их в
программе Mathematica, мне же остается только
порисовать:
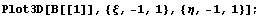
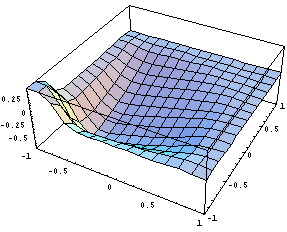
Вот одна из первых производных:
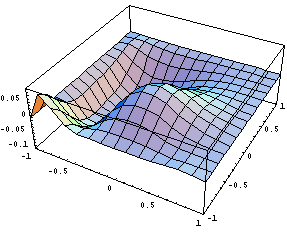
Эта статья написана, чтобы показать как
учитывать производные в качестве степеней
свободы в конечных элементах и проверить
предложенный в предыдущей статье метод
построения конечномерных пространств функций.
Эти результаты, в отличие от предыдущих, не
проходили проверки программированием и вызывают
некоторые сомнения. Особенно это касается
треугольных элементов, с которыми наверное стоит
еще потрудиться. Но автор не планирует в
ближайшее время заниматься стержнями и
оболочками. Может быть уважаемый Сергей Курков
захочет попробовать вставить элементы высокой
точности в свою прекрасную программу
"Зенит".
В следующей статье рассмотрим иерархические
моды, которые позволяют повышать точность
элементов с минимальными дополнительными
вычислениями. Но главное, по мнению автора,
совсем за небольшую дополнительную плату,
позволяют вычислить оценку ошибки решения,что
позволит снизить недоверие к численным методам и
сделает вычисления еще более совершенным
инструментом.
- Зенкевич О.,Морган К.Конечные элементы
и аппроксимация:Пер.с англ.-М.: Мир,1986.
- Партон В.З.,Перлин П.И. Методы
математической теории упругости: М.: Наука,1981.
Санкт-Петербург,апрель-май 2000 года
В начало |

