Список встроенных функций

Возможно также представить графически элементы вектора. Такой график показан на Рисунке 4. Для его создания сделайте следующее:

• Определите дискретную переменную i,  являющуюся  нижним индексом каждого элемента, которые нужно начертить.
• Определите вектор y_i. Используйте клавишу левой скобки [ , чтобы создать нижний индекс.
• Нажмите @  для создания бланка графика.
• Разместите в среднем поле вертикальной оси и i в среднем поле горизонтальной оси.
• Нажмите [F9], чтобы увидеть график.

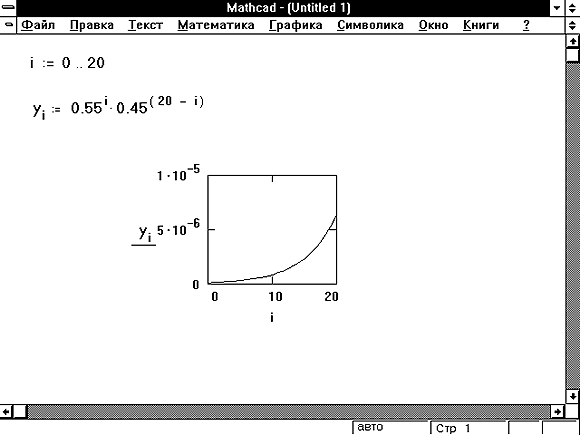
Рисунок 4: Графическое представление вектора.

Нижние индексы должны быть неотрицательными целыми числами (или целыми, большими или равными ORIGIN, если ORIGIN 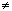0.) Это означает, что абсцисса может принимать только целочисленные значения. Если нужно использовать дробные или отрицательные значения на оси абсцисс, стройте график функции, как на Рисунке 2 или отображайте один вектор относительно другого, как описано в следующем разделе.

Если имеется набор данных, для которых нет подходящей функциональной связи, как на Рисунке 4, но их слишком мало, чтобы использовать файлы данных, можно использовать таблицу ввода для создания вектора.

Отображение одного вектора относительно другого

Рисунок 5 показывает, как отобразить один вектор относительно другого. Векторы не должны быть одной длины. Требуется только:

• Оба вектора должны совместно использовать один и тот же нижний индекс. Например, нельзя начертить x_i относительно  y_j, потому что i и j — различные индексы.
• Каждое значение нижнего индекса должно соответствовать некоторому элементу в каждом векторе. Например, если x имеет только два элемента, и y имеет восемь элементов, а дискретная переменная изменяется от 0 до 7, появится сообщение об ошибке “индекс вне границ” .

Чтобы создать график, показанный на Рисунке 5, сделайте следующее:

• Определите дискретную переменную i,  являющуюся  нижним индексом каждого отображаемого элемента.
• Определите массивы x_i и y_j. Используйте клавишу левой скобки [ для  написания  индекса.
• Нажмите @ , чтобы создать бланк графика.
• Поместите y_i в среднем поле оси ординат и x_i в среднем поле оси абсцисс.
• Нажмите [F9], чтобы увидеть график.

Хотя вектор x на Рисунке 5 представляет набор равномерно располагаемых значений, это не является необходимым. Требуются только, чтобы индекс i представлял собой равномерно расположенные целые числа. Подобного ограничения не существует для x_i. Это позволяет использовать на оси абсцисс не только целые числа и при этом удовлетворить требованию целочисленности нижних индексов. На Рисунке 5 y_i вычисляется непосредственно через x_i. Можно было бы вычислять x и y независимо из третьей переменной. Если только два вектора используют одну и ту же дискретную переменную, можно отобразить их на одном графике.

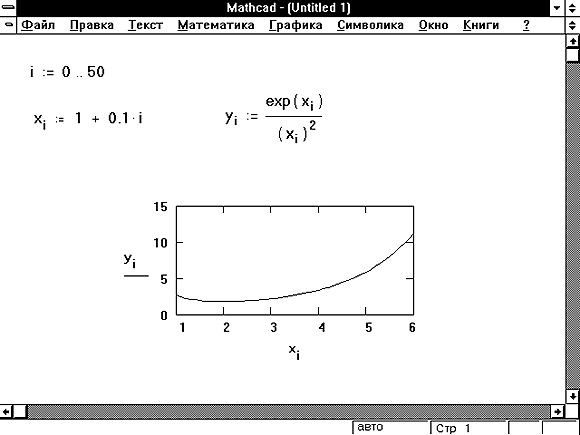
Рисунок 5: Совместное графическое представление двух векторов.

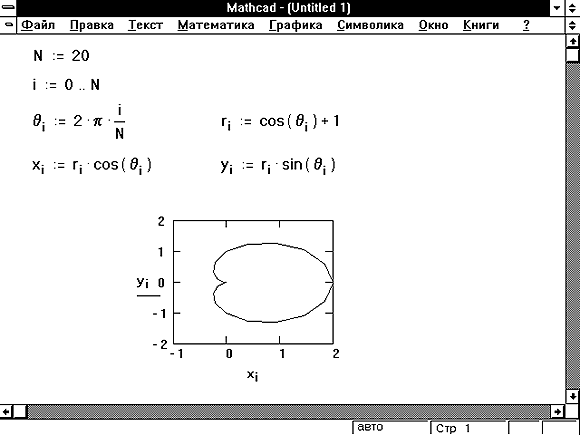
Рисунок 6: Два вектора, вычисленные независимо.

Рисунок 6 показывает график в полярных координатах, в котором и x и y зависят от переменных r и q. На Рисунке 6 с использованием векторов решена та же самая задача, которая была решена с использованием функций на Рисунке 3.

Обратите внимание, что на Рисунке 6 дискретная переменная i должна принимать целочисленные значения и используется, чтобы определить вектор q равномерно располагаемых нецелых чисел. На Рисунке 3 q определялся непосредственно как дискретная переменная. Это было возможно потому, что функции не требуют целочисленных аргументов, как векторы требуют целочисленных нижних индексов.

Графическое представление файлов данных

Можно использовать функции READ и READPRN Mathcad, чтобы импортировать данные из текстовых файлов в ASCII-формате из любой электронной таблицы, базы данных или текстового редактора, способных к экспорту данных в текстовом формате. После импорта данных Mathcad отображает их так же, как если бы это были данные, созданные в Mathcad.

Например, вот как можно отобразить данные из электронной таблицы:

• Сохраните электронную таблицу как текстовый файл ASCII с расширением .prn .
• Используйте функцию READPRN, чтобы импортировать .prn  файл в Mathcad как матрицу. См. подраздел “Считывание матрицы с помощью функции READPRN” .
• Рисунок 7 показывает процесс графического представления векторов из данных, импортируемых из .prn  файла.

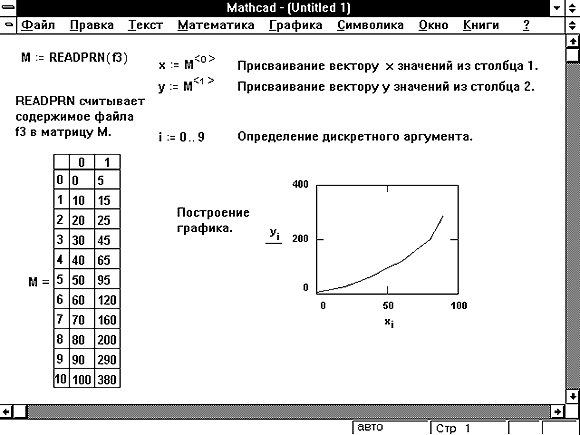
Рисунок 7: Графическое представление импортированных векторов

Графическое представление других выражений

Рисунки 2-6 показывают некоторые из наиболее употребительных типов графиков. Еще один пример на Рисунке 12 показывает нанесение на график константы, используемой как риска на графике другой функции. Возможные графики не исчерпываются этими примерами. Можно отобразить на графике любое множество точек, координаты которых вычисляются любой парой выражений, лишь бы только эти выражения использовали одни и те же дискретные аргументы.

Список встроенных функций