Команда Motion
Команда motion выводит уравнения и решает
задачу движения для заданного физического
объекта и типа движения а также обращается к
команде geom_physдля вывода на дисплей геометрии
задачи и результирующего движения.
Приведем конкретные примеры. Будем решать
задачи движения одиночных тел в трех измерениях,
поэтому вводим соответствующую команду
инициализации пакета
> physics[ph_init](1,3,object=body);
![[Maple Math]](images/labs7.gif)
Задаем тип объекта (возможно задать sphere (сфера),
hemisphere (полусфера), cone (конус), acone (асимметричный
(эллиптический) конус), ellipsoid (эллипсоид),
прямоугольный параллелепипед (cuboid) и цилиндр
(cylinder).
> Object:=ellipsoid;
![[Maple Math]](images/labs8.gif)
Задаем тип движения. Возможно колебательное
движение (pendulum), вращение вокруг закрепленной
точки (gyroscope), качение по шероховытой плоскости
(roll), качение внутри сферической поверхности
(sphere_roll) скольжение по абсолютно гладкой
плоскости (slip).
> Type:=pendulum;
![[Maple Math]](images/labs9.gif)
Задаем геометрические параметры физического
объекта, необходимые для расчета его массы,
момента и центра инерции, а также самого
движения.
> Axes:=[3,5,8];
![[Maple Math]](images/labs10.gif)
а также физические параметры тела и поля.
плотность (по умолчанию 10 г/см3)
> #rho:=7.8;
Напряженность силового поля (по умолчанию [0,0,980]
- для гравитачионного поля вдоль вертикальной
оси (R3).
> #gravity:=[0,0,980];
Теперь задаем начальное положение центра
инерции тела относительно начала лабораторной
системы координат, например
> Center:=[1,2,-5];
![[Maple Math]](images/labs11.gif)
и начальный поворот тела (связанной с ним
эйлеровой системы координат) относительно
лабораторной (декартовой системы координат).
> Angles:=[Pi/3,Pi/6,Pi/4];
![[Maple Math]](images/labs12.gif)
Задаем начальные угловые скорости
> Velocity:=[16];
![[Maple Math]](images/labs13.gif)
> Mass:=rho*physics[body_inert](m,Axes,object='ellipsoid','volume');
![[Maple Math]](images/labs14.gif)
и момент инерции
> Inertia:=physics[body_inert](Mass,Axes,object='ellipsoid');
![[Maple Math]](images/labs15.gif)
Теперь можно нарисовать геометрию задачи
пользуясь ключом static в команде motion
> motion(Axes,[op(Center),op(Angles)], Velocity,
intensity=gravity, type=Type, object=Object,static, style=contour, contours=30,
color=wheat, axes=normal, scaling=constrained, labels=[r1,r2,r3],
labelfont=[TIMES,BOLD,14]); ![[Maple Plot]](images/labs16.gif)
Вы можете подобрать стили оформления рисунка
по вашему вкусу. В случае задания колебательного
движения ( pendulum ) осью вращения является ось r1
лабораторной системы координат. На рисунке
помимо главных осей инерции эллипсоида (которые
являются также осями элеровой системы координат)
изображено расстояние d от центра инерции до
оси вращения, входящее в уравнения движения.
Направляющие косинусы n оси вращения в
эйлеровой системе координат и расстояние d
определяются при помощи соотношений.
> n0:=physics[conv_coord]((r,v)->r,[1,0,0],move_c(v),frame=inv_zveer,angles=Angles);
l0:=physics[conv_coord]((r,v)->r,Center,move_c(v),frame=zveer,angles=Angles);
d0:=evalf(sqrt(evalm([0,l0[2],l0[3]]&*[0,l0[2],l0[3]])));
![[Maple Math]](images/labs17.gif)
![[Maple Math]](images/labs18.gif)
![[Maple Math]](images/labs19.gif)
Начальный угол отгносительно равновесного
положения, связанный с начальным смещением
центра инерции относительно оси вращения
> q01:=evalf(simplify(arctan(-l0[2],-l0[3])));
![[Maple Math]](images/labs20.gif)
Теперь можно вывести уравнения движения в
символьной форме
> motion([a,b,c],[x,y,z,op(Angles)],[omega[theta]],'density'=rho,'intensity'=[0,0,g],
type=Type,object=Object,equations);
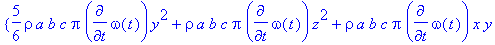
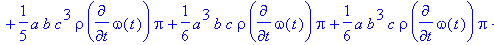
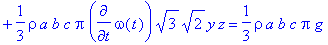
![[Maple Math]](images/labs23.gif)
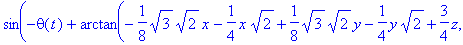
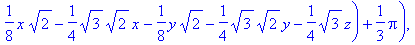
![[Maple Math]](images/labs25.gif)
и после подстановки численных значений
> motion(Axes,[op(Center),op(Angles)],Velocity,type=Type,object=Object,equations);
![[Maple Math]](images/labs26.gif)
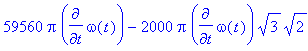
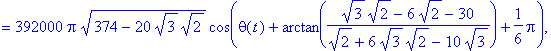
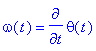 ![[Maple Math]](images/labs28.gif)
Численное решение задачи
> Q:=motion(Axes,[op(Center),op(Angles)],Velocity,type=Type,object=Object,solution);
![[Maple Math]](images/labs29.gif)
Строим график зависимости угла от времени
> plot(Q[1],0..3);
![[Maple Plot]](images/labs30.gif)
Генерируем анимацию движения физического
маятника
> motion(Axes,[op(Center),op(Angles)], Velocity, type=Type,
object=Object, style=patch, lightmodel=`light4`, shading=`zhue`, frames=35, points=30,
scaling=constrained);
  
|

