  В
этой главе показано много примеров, использующих
символ нижнего индекса и дискретные аргументы. В
Главе “Векторы и
матрицы” содержится много примеров,
использующих векторную запись без нижних
индексов. Здесь есть важная деталь. Если
использовать нижние индексы, когда они не
требуются, или наоборот, можно не получить
желаемый результат.
Нижние индексы обращаются к отдельным
элементам массива. Когда дискретные аргументы
используются как нижние индексы, подобно Mi,
j, Mathcad пробегает элементы массива поодиночке.
Имя без нижних индексов относится к массиву
целиком.
Существуют некоторые элементарные правила
относительно того, когда использовать нижние
индексы:
- Чтобы обратиться к отдельному элементу массива,
используйте числа как нижние индексы. Например,
чтобы увидеть элемент матрицы (2,3), напечатайте M[2,3=.
- Чтобы обратиться к массиву в целом, используйте
имя массива без нижних индексов. (Термин массив
означает или вектор или матрицу). Имя массива без
нижних индексов следует использовать для
умножения одной матрицы на другую, для
применения функции mean к массиву, или для
просмотра вектора или матрицы целиком — всех
случаев, когда следует обращаться с массивом как
с целым. Например, чтобы просмотреть на Рисунке 13
матрицу M целиком, напечатайте M=.
- Чтобы обратиться к каждому из элементов массива
последовательно, используйте имя массива с
дискретным аргументом в качестве нижнего
индекса. Это полезно при определении элементов
матрицы с использованием какой-либо формулы.
Например, чтобы определить матрицу M из
Рисунка 13, напечатайте три формулы:
i: 0;3
j: 0;3
M [i, j: i * j |
Рисунок 13 показывает некоторые примеры
употребления имен массивов с использованием
нижних индексов и без.

Рисунок 13: Имена массивов с использованием
нижних индексов и без.
Итерационные вычисления с нижними индексами и
без
Часто быстрее использовать векторные операции,
чтобы выполнить многократные вычисления, чем
делать их поэлементно с помощью дискретного
аргумента. Это обсуждается более подробно в
разделе “Выполнение
параллельных вычислений” . К сожалению, не все
многократные вычисления могут быть выполнены
как векторные операции. Например, рекурсивные
вычисления, обсужденные ранее в этой главе, не
могут быть выполнены посредством векторных
операций.
Чтобы решить, следует ли переписать формулу с
нижними индексами, используя векторную запись и
оператор векторизации, проверьте следующее:
- Если все нижние индексы в формуле одни и те же,
то, вероятно, вычисление будет выполнено быстрее
с использованием векторных операций. Например,
рассмотрим формулу:
xi := ri cos(qi) cos(qi)
Поскольку эта формула не содержит никакого
другого нижнего индекса, кроме i, она может
быть перезаписана с оператором векторизации ( [Ctrl][-]
):
x :=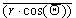
- Если формула содержит различные нижние индексы,
или если в качестве нижнего индекса используется
выражение, вычисление, вероятно, не может быть
выполнено с использованием векторных операций.
Например, рекурсивные вычисления включают
нижние индексы i и i -1 в одной формуле. Так
как нижние индексы различаются, и так как второй
нижний индекс является выражением, это
вычисление не может быть выполнено с
использованием векторных операций.
- Если дискретный аргумент появляется где-либо в
формуле кроме нижнего индекса, формула не может
быть переписана c использованием векторных
операций. Например, ниже переменная q не может
быть определена через оператор векторизации,
поскольку в правой части формулы дискретный
аргумент i не является индексом, а участвует в
вычислении.
qi := 0.1 i i
Рисунок 14 показывает то же самое
преобразование полярных координат в декартовы,
что и Рисунок 6, выполненное двумя способами: с
использованием нижних индексов и через операцию
векторизации. В Mathcad второй метод намного
быстрее.

Рисунок 14: Выполнение многократных
вычислений с помощью векторизации.
  
|

