Список встроенных функций

Рекурсивные вычисления применяются для решения конечно-разностных уравнений типа тех, которые возникают в задачах вычисления сложного процента, Марковских процессах и многих уравнениях фазовых состояний. Они могут также использоваться для получения приближенных решений для некоторых дифференциальных уравнений. В рекурсивных вычислениях определяется первый элемент массива и затем вычисляются последовательные элементы, основанные на первом элементе. Этот раздел описывает три типа рекурсивных вычислений: с одиночной переменной, с множественными переменными, и с вектором.

Рекурсивные вычисления с одной переменной

Классический метод для вычисления квадратных корней состоит в следующем:

• Чтобы найти 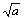, начните с предполагаемого значения, которое можно рассматривать как приближение к истинному.
• Вычислите новое приближение, основанное на старом приближении, по формуле

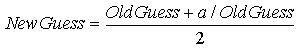• И так далее, пока приближения не сойдутся к ответу.

Рисунок 10 показывает, как выполнить этот метод в Mathcad.

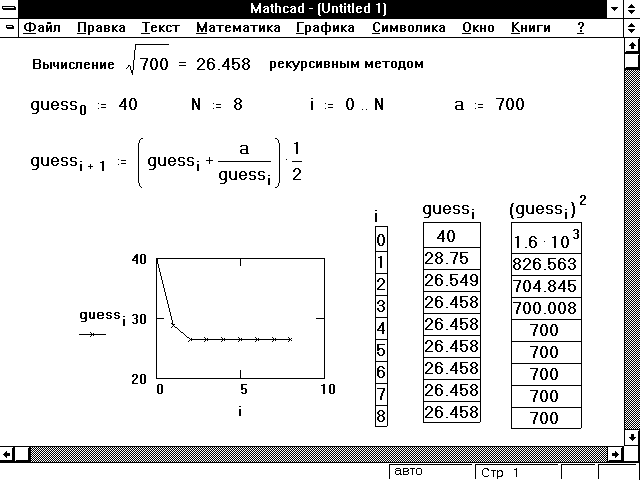
Рисунок 10: Использование рекурсивных вычислений для вычисления квадратного корня.

Характерные особенности этого примера:

• Начальное значение определено как нулевой элемент массива, guess₀.
• Каждый элемент guess_i+1 определяется через предыдущий.

Зависимость элементов массива от предварительно вычисленных элементов массива — та особенность, которая отличает рекурсивные вычисления от более простого многократного вычисления, обсужденного в предыдущем разделе.

Рекурсивные вычисления с несколькими переменными

Удобно использовать запись вектора Mathcad, чтобы выполнить многократные вычисления нескольких переменных одновременно. Эта разновидность рекурсивных вычислений — мощный метод для решения системы уравнений в конечных разностях.

При выполнении многократных вычислений нескольких переменных на каждом шаге вычисляются значения переменных на основе всех их предыдущих значений. Нельзя сделать это с отдельными уравнениями, потому что, когда Mathcad видит формулу с дискретным аргументом, он пытается вычислить её для каждого значения дискретного аргумента перед переходом к следующему уравнению. Значит, следует создать одну формулу, которая выполняет вычисления со всеми переменными одновременно.

Например, рассмотрим модель эпизоотии с четырьмя переменными: через i обозначим число инфицированных животных, через s — число восприимчивых, через d — число умерших, через r — число выздоровевших и приобретших иммунитет. Четыре уравнения, которые связывают эти переменные в каждый момент:

il+1 = 0.0001 sl il sl+1 = sl - 0.0001 sl il dl+1 = dl + 0.55 il rl+1 = rl + 0.45 il

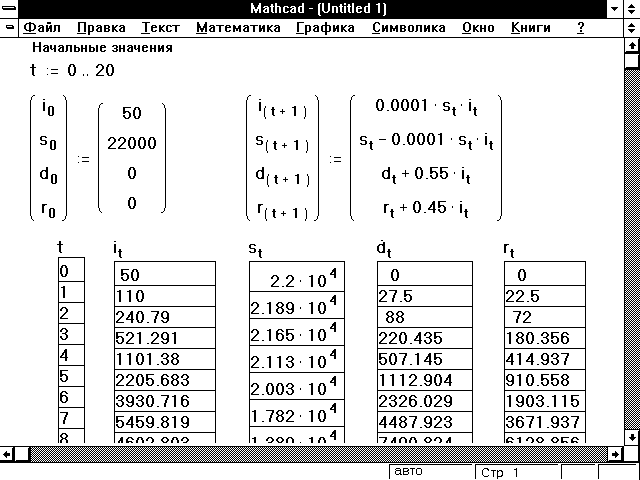
Рисунок 11: Вычисления в модели распространения инфекции.

Рисунок 11 показывает, как выполнить одновременные вычисления, используя эти уравнения.

Сделаем одно очень важное замечание относительно этого примера: все индексы l+1 собраны по левую сторону уравнения. Правая сторона содержит только индекс l. Mathcad вычисляет все выражения справа перед выполнением любых присваиваний левой стороне. Это означает, что ничто справа не может зависеть ни от чего слева.

Рекурсивные вычисления с вектором

Возможно также выполнять рекурсивные вычисления, начинающиеся с вектора и возвращающие каждый раз новый вектор. Этот тип многократных вычислений использует начальный вектор и оператор верхнего индекса Mathcad.

Марковский процесс — пример задачи, которая приводит к рекурсивным вычислениям вектора. Марковский процесс начинает с вектора v, который задает начальные значения некоторых количеств, например, число избирателей, планирующих голосовать за различных кандидатов, число грузовиков в региональных ведомствах компании, сдающей в прокат грузовики, или долей различных компаний на рынке. Каждый шаг в процессе Маркова вычисляет новый вектор, умножая предыдущий вектор на переходную матрицу A. Рисунок 12 показывает, как задать процесс Маркова. Эта методика использует верхние индексы, чтобы индексировать весь столбец матрицы сразу. Чтобы создать верхний индекс, нажмите [Ctrl]6. Появится поле между угловыми скобками: < > .

Вот как записать уравнения из Рисунка 12:

• Определите переходную матрицу A. Напечатайте A, нажмите клавишу двоеточия (:) и создайте 3x3 матрицу. Чтобы создать матрицу, выберите Матрицы из меню Математика.

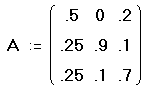
• Щёлкните справа от матрицы и напечатайте v. Затем нажмите [Ctrl]6. Напечатайте 0 в поле для верхнего индекса.

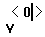
• Завершите определение начального вектора. Нажмите клавишу двоеточия (:), затем выберите Матрицы из меню Математика. Укажите, что создаётся матрица с тремя строками и одним столбцом. Потом заполните ячейки матрицы.

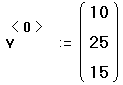
• Напечатайте k:1;8. Это задаст дискретный аргумент k, чтобы выполнить восемь вычислений.

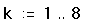
• Чтобы выразить k-тый вектор через (k-1)-ый, напечатайте v [Ctrl] 6 k. Затем напечатайте двоеточие (:) для символа определения. Завершите формулу, напечатав после символа определения: A*v[Ctrl] 6 k-1 .

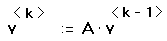
• Чтобы увидеть восьмой (последний) столбец матрицы, напечатайте v [Ctrl] 68=.

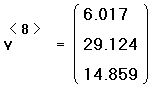
• Чтобы увидеть все векторы как столбцы матрицы, напечатайте v=. Обратите внимание, что в изображении справа отображаются не все столбцы.

Рисунок 12: Рекурсивные вычисления вектора к модели Марковского процесса.

Оператор верхнего индекса фактически отыскивает или определяет один столбец в матрице. Определение v^<k> через v^<k-1> фактически выражает каждый столбец матрицы через предшествующий столбец. В последнем равенстве на Рисунке 12 показана матрица, составленная из этих столбцов.

Список встроенных функций