  Этот раздел показывает,
как использовать дискретные аргументы для
выполнения многократных вычислений. Этот раздел показывает,
как использовать дискретные аргументы для
выполнения многократных вычислений.
Многократные вычисления по дискретному
аргументу
Простейший вид многократных вычислений в Mathcad
— простое обобщение скалярных вычислений. Любое
вычисление, которое можно выполнить один раз,
можно выполнить и над диапазоном значений.
Например, предположим, что необходимо создать
список значений x и y для точек на кривой r =
cos(q) + 1. Идея состоит в
следующем:
- q должен принимать значения
между 0 и 2p .
- Для каждого q
соответствующее значение r дается формулой
r = cos(q) + 1.
- Для каждых r и q
соответствующие декартовы координаты x и y
даются формулами x = r
 cos(q) и y = r cos(q) и y = r sin(q). sin(q).
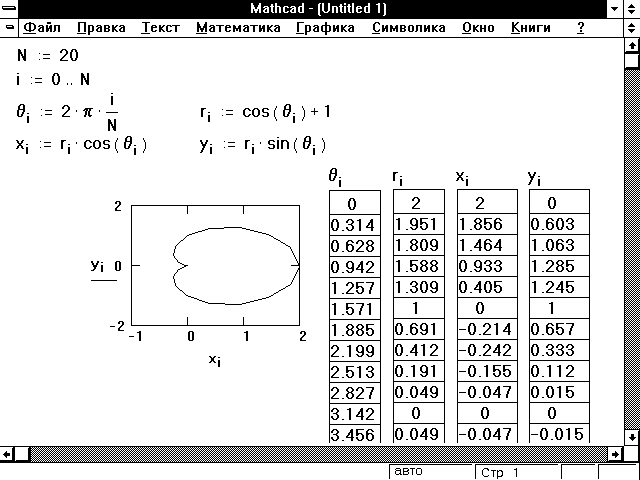
Рисунок 6: Переход от полярных к декартовым
координатам.
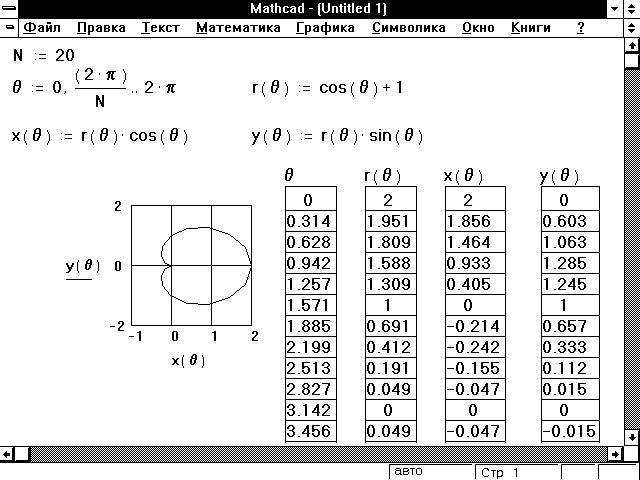
Рисунок 7: То же самое, что и на рисунке 6, но с
использованием функций.
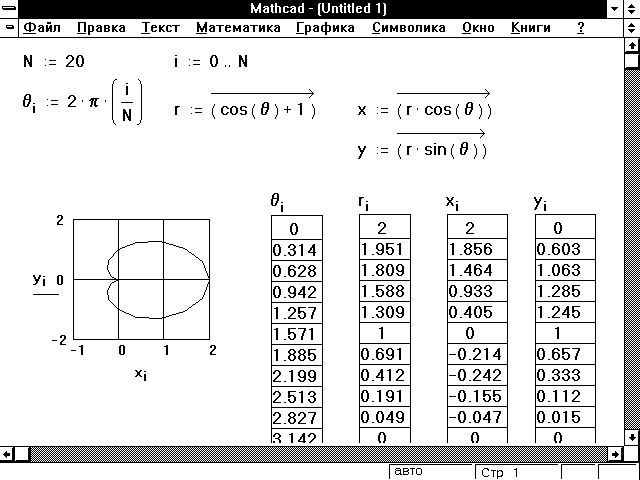
Рисунок 8: Использование оператора
векторизации для создания полярного графика.
Стратегия решения этой проблемы проста:
создайте дискретный аргумент i и затем
вычислите q, r, x и y для
каждого значения qi.
Формула для определяет q для
значений от 0 до 2p с шагом 2p/N . Для создания остальных
формул только проставьте индекс i при каждой
переменной в формуле. Рисунок 6 показывает
результат.
Обратите внимание, что в этом примере i, а не q, определен как дискретный
аргумент. Поскольку i принимает только
целочисленные значения, это — допустимый нижний
индекс. С другой стороны, q
принимает дробные значения, следовательно, она
не может использоваться как нижний индекс. Во
многих случаях возможно избежать этого
дополнительного шага, используя функции вместо
векторов. Рисунок 7 показывает, как создать
кардиоиду, показанную на Рисунке 6, при помощи
функций вместо векторов.
Используя векторную запись и оператор
векторизации, удаётся избежать использования
нижнего индекса в последних трех уравнениях из
Рисунка 6. Рисунок 8 показывает пример того, как
это достигается.
Формулы, которые используют векторную запись
вместо нижних индексов, обычно вычисляются
намного быстрее. Более подробно см. Главу “Векторы и матрицы”.
Множественные дискретные аргументы и двойные
индексы
Если в формуле используется два дискретных
аргумента, Mathcad пробегает через каждое значение
каждого дискретного аргумента. Это можно
использовать для определения матриц. Например,
чтобы определить матрицу x размера 5x5, где xi,j
= i + j, напечатайте формулы:
Обратите внимание, что не нужно
печатать [Space], чтобы покинуть нижний индекс в
этом случае. Напечатав : , Вы одновременно
покидаете нижний индекс и создаете символ
определения.
Рисунок 9 показывает результат печати
вышеупомянутых формул. Обычно лучше всего
отобразить матрицу в форме, показанной на
Рисунке 9. Если вместо того, чтобы напечатать x=,
записать x[i,j=, Mathcad отобразит одну длинную таблицу
вывода с 25 числами. Такую таблицу часто трудно
интерпретировать. Подобная проблема возникает,
когда в графике используется пара дискретных
аргументов.
Выражение для xi,j вычисляется для каждого
значения каждого дискретного аргумента, всего 25
вычислений. Результат — матрица, показанная
внизу рисунка, с 5 строками и 5 столбцами. Элемент
в i-ой строке и j-ом столбце этой матрицы
равен i + j.

Рисунок 9: Определение матрицы.
Обратите внимание, что, если два дискретных
аргумента имеют значения m и n
соответственно, формула, использующая оба
дискретных аргумента, будет вычислятьcя m n раз. Если
использовать два дискретных аргумента в таблице
вывода, Mathcad покажет эти m n раз. Если
использовать два дискретных аргумента в таблице
вывода, Mathcad покажет эти m n результата в длинной
таблице с ячейкой для каждого результата. Если
два дискретных аргумента используются в графике,
Mathcad отобразит по одной точке для каждого из m n результата в длинной
таблице с ячейкой для каждого результата. Если
два дискретных аргумента используются в графике,
Mathcad отобразит по одной точке для каждого из m n
результатов. n
результатов.
  
|

