Постановка задачи
приближения функции по методу интерполяции ~ Интерполяционный многочлен Лагранжа ~ Разделенные разности~ Интерполяционный
многочлен Ньютона~ Оценка погрешности
интерполяции
Постановка задачи интерполяции
функций.
Пусть функция y = f(x) задана таблицей своих
значений:
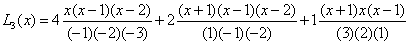 , i=0,1,...n. Требуется найти
многочлен степени n, такой, что значения
функции и многочлена в точках таблицы совпадают: , i=0,1,...n. Требуется найти
многочлен степени n, такой, что значения
функции и многочлена в точках таблицы совпадают:
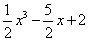 , i=0,1,... n. , i=0,1,... n.
Справедлива теорема о существовании и
единственности интерполяционного многочлена.
Одна из форм записи интерполяционного
многочлена - многочлен Лагранжа:
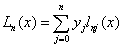 , где , где
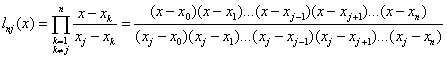
Многочлен 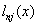 представляет собой
многочлен степени n , удовлетворяющий условию представляет собой
многочлен степени n , удовлетворяющий условию
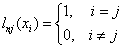 . .
Таким образом, степень многочлена 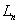 равна n и при
равна n и при 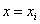 в сумме обращаются в
нуль все слагаемые, кроме слагаемого с номером в сумме обращаются в
нуль все слагаемые, кроме слагаемого с номером 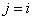 , равного , равного 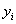 .
Поэтому многочлен Лагранжа является
интерполяционным. .
Поэтому многочлен Лагранжа является
интерполяционным.

ПРИМЕР 1.Построение многочлена
Лагранжа.
Другая форма записи интерполяционного
многочлена - интерполяционный многочлен Ньютона
с разделенными разностями. Пусть
функция f задана с произвольным шагом и
точки таблицы занумерованы в произвольном
порядке. Величины
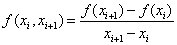 называют
разделенными разностями первого порядка.
Разделенные разности второго порядка
определяются формулой: называют
разделенными разностями первого порядка.
Разделенные разности второго порядка
определяются формулой:
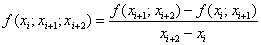 . .
Определение разделенной разности порядка 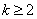 таково: таково:
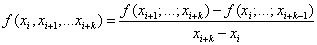 . .
Используя разделенные разности,
интерполяционный многочлен Ньютона можно
записать в следующем виде:
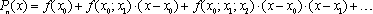
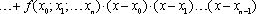

ПРИМЕР 2. Построение
интерполяционного многочлена Ньютона с
разделенными разностями.
Величину 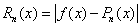 называют погрешностью
интерполяции или остаточным членом
интерполяции. называют погрешностью
интерполяции или остаточным членом
интерполяции.
Оценка погрешности интерполяции.
Если функция n+1 раз на отрезке [a,b] ,
содержащем узлы интерполяции 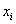 ,
i=0,1,...n, то для погрешности интерполяции
справедлива оценка: ,
i=0,1,...n, то для погрешности интерполяции
справедлива оценка:
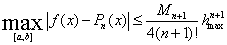 . Здесь . Здесь 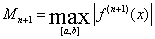 , ,
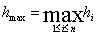 . .
Эта оценка показывает, что для достаточно
гладкой функции при фиксированной степени
интерполяционного многочлена погрешность
интерполяции стремится к нулю не медленнее, чем
величина, пропорциональная 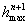 .
Этот факт формулируют так: интерполяционный
многочлен степени n аппроксимирует функцию с
(n+1) порядком точности относительно .
Этот факт формулируют так: интерполяционный
многочлен степени n аппроксимирует функцию с
(n+1) порядком точности относительно 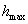 . .

ПРИМЕР 3. Использование
остаточного члена интерполяции.
В практическом плане формула Ньютона обладает
преимуществами перед формулой Лагранжа.
Предположим, что в необходимо увеличить степень
многочлена на единицу, добавив в таблицу еще один
узел 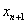 . При использовании
формулы Лагранжа это приводит к необходимости
вычислять каждое слагаемое заново. Для
вычисления . При использовании
формулы Лагранжа это приводит к необходимости
вычислять каждое слагаемое заново. Для
вычисления 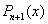 достаточно добавить к достаточно добавить к
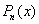 лишь очередное слагаемое: лишь очередное слагаемое: 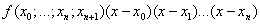 . Если функция f достаточно
гладкая, то справедливо приближенное равенство . Если функция f достаточно
гладкая, то справедливо приближенное равенство 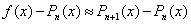 . Это равенство можно использовать
для практической оценки погрешности
интерполяции : . Это равенство можно использовать
для практической оценки погрешности
интерполяции :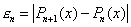 . .

|

