Пример 1 ~ Пример 2 ~ Пример 3
Пример 1. Построение многочлена Лагранжа.
По таблице построим интерполяционный
многочлен:
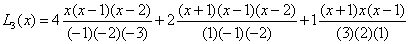 = = 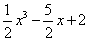

Пример 2. Построение интерполяционного
многочлена Ньютона с разделенными разностями.
По таблице значений функции из
ПРИМЕРА 1 построим интерполяционный многочлен
Ньютона. Составим таблицу разделенных разностей:
Теперь запишем интерполяционный
многочлен Ньютона:
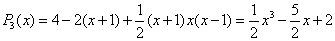
Отметим, что в силу единственности
интерполяционного многочлена, мы получили тот же
самый многочлен, что в ПРИМЕРЕ 1.
Теоретическая справка

Пример 3. Использование остаточного члена
интерполяции.
Пусть требуется составить таблицу
функции 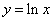 на отрезке [1,10].
Какой величины должен быть шаг h, чтобы при
линейной интерполяции значение функции
восстанавливалось с погрешностью не меньшей на отрезке [1,10].
Какой величины должен быть шаг h, чтобы при
линейной интерполяции значение функции
восстанавливалось с погрешностью не меньшей 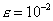 ? ?
Запишем остаточный член интерполяции
при линейной интерполяции
 . .
Так как 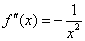 , то , то 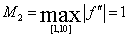 . Тогда . Тогда 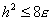 . Следовательно, . Следовательно, 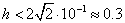 . .
Теоретическая справка

|

