Теорема
Пуассона ~ Локальная теорема
Муавра-Лапласа ~ Интегральная теорема
Муавра-Лапласа ~ Теорема Бернулли
Теорема Пуассона. При большом
количестве испытаний вычисления по формуле
Бернулли становятся затруднительными. Однако в
ряде случаев их можно заменить более простыми асимптотическими
формулами. Одна из них основана на теореме
Пуассона.
Если число испытаний n ® 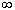 и p
® 0 так, что np ® l , l > 0, то и p
® 0 так, что np ® l , l > 0, то 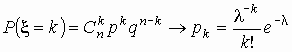
при любых k = 0, 1, 2, … .
Это означает, что при больших n и малых p
вместо вычислений по точной формуле
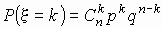 
можно воспользоваться приближенной формулой
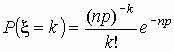 . .
На практике пуассоновским приближением
пользуются при npq= np(1-p) < 9. Исследуем
точность асимптотической формулы Пуассона на
следующем примере.
ПРИМЕР 1 . Точность формулы
Пуассона.
В здании 1000 лампочек. Вероятность выхода из
строя одной лампочки в течение года p =0.003.
Найдем вероятность того, что в течение одного
года выйдет из строя более трех ламп. Выполним
вычисления используя формулу Бернулли и по
теореме Пуассона.
Для вычисления вероятности по формуле Бернулли
используем формулу
P(x > 3) = 1- P(x 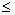 3) = 1- Fx (3), 3) = 1- Fx (3),
где Fx (x) - функция
распределения для биномиального распределения.
Для вычисления вероятности по теореме Пуассона
используем формулу
P(m > 3) = 1- P(m
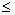 3) = 1- Fm (3),
3) = 1- Fm (3),
где Fm (x) - функция
распределения Пуассона с параметром l
= np = 3.
Выполним те же вычисления для p = 0.3 и n = 10
(l = np =3).
Локальная теорема Муавра-Лапласа. Если
npq > 9, то для расчетов используют
приближение Муавра-Лапласа
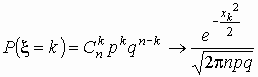 , ,
где 0 < p < 1 , величина 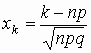 ограничена при n ® ограничена при n ® 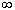 . .
Требование ограниченности величины xk
означает, что при n ® 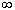 величина величина
k тоже должна расти вместе с величиной n.
Точность формулы
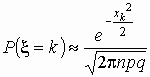
растет, как с ростом величин n и k, так и
по мере приближения к 0.5 величин p и q.
Исследуем точность асимптотической формулы
Муавра-Лапласа на следующем примере.
ПРИМЕР 2 . Точность формулы
Муавра-Лапласа.
Вычислим вероятность того, что случайная
величина, имеющая биномиальное распределение,
принимает значение, равное n/2 . Выполним
вычисления для n = 10, 20, 50. Сравним результаты
вычислений по формуле Бернулли и по приближенной
формуле Муавра-Лапласа.
Интегральная теорема Муавра-Лапласа.
При n ® 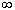 для схемы Бернулли
при любых a и b справедлива формула для схемы Бернулли
при любых a и b справедлива формула
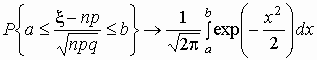 . .
Отсюда следует, что вероятность того, что число
успехов в n испытаниях Бернулли заключено
между k1 и k2, можно вычислить
по формуле
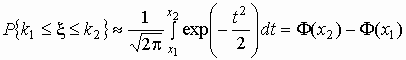 , ,
где 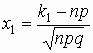 , , 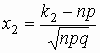 , , 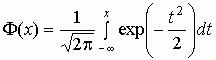 - функция Лапласа. - функция Лапласа.
Точность этой приближенной формулы растет с
ростом n. Если значение npq сравнительно
невелико, то лучшее приближение дает формула
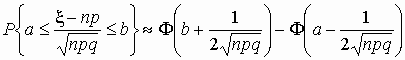 , ,
и для вычисления вероятности того, что число
успехов в n испытаниях Бернулли заключено
между k1 и k2, можно
использовать формулу
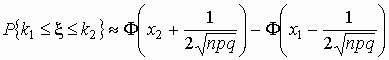 , ,
где 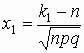 , , 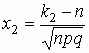 . .
ПРИМЕР 3 . Точность
интегральных формул Муавра-Лапласа.
Вероятность рождения мальчика p = 0.51, а
девочки - q = 1 - p = 0.49. Найдем вероятность
того, что среди 10 000новорожденных мальчиков будет
не менее 4 000 и не более 5000. Вычисления проведем по
формуле Бернулли и по приближенным интегральным
формулам Муавра-Лапласа.
Теорема Бернулли. Если x
- число успехов в n испытаниях Бернулли с
вероятностью p успеха в одном испытании, то
для любого e > 0 справедливо
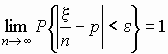 . .
Это означает, что с ростом числа испытаний n
относительная частота успехов x
/n приближается к вероятности p успеха в
одном испытании.
Определим, сколько нужно произвести испытаний,
чтобы с вероятностью, больше или равной b, отклонение относительной частоты
успехов x /n от вероятности p
было меньше e . Т.е. найдем n, для
которого выполняется неравенство
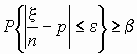 . .
Доказано, что для числа n, которое
обеспечивает выполнение этого неравенства,
справедливо
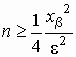 , ,
где xb - решение
уравнения 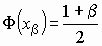 . .
Следует обратить особое внимание на
замечательный факт - искомое значение n не
зависит от p!
ПРИМЕР 4. Производитель
утверждает, что вероятность отрицательного
отношения покупателя к новому товару невелика.
Сколько нужно опросить человек, чтобы с
вероятностью не менее 0.9 можно было утверждать,
что относительная частота отрицательного
отношения к новому товару отличается от
заявленной производителем не более, чем на 0.01.

|

